Нейронные сети для начинающих. Часть 1 / Habr

Привет всем читателям Habrahabr, в этой статье я хочу поделиться с Вами моим опытом в изучении нейронных сетей и, как следствие, их реализации, с помощью языка программирования Java, на платформе Android. Мое знакомство с нейронными сетями произошло, когда вышло приложение Prisma. Оно обрабатывает любую фотографию, с помощью нейронных сетей, и воспроизводит ее с нуля, используя выбранный стиль. Заинтересовавшись этим, я бросился искать статьи и «туториалы», в первую очередь, на Хабре. И к моему великому удивлению, я не нашел ни одну статью, которая четко и поэтапно расписывала алгоритм работы нейронных сетей. Информация была разрознена и в ней отсутствовали ключевые моменты. Также, большинство авторов бросается показывать код на том или ином языке программирования, не прибегая к детальным объяснениям.
Поэтому сейчас, когда я достаточно хорошо освоил нейронные сети и нашел огромное количество информации с разных иностранных порталов, я хотел бы поделиться этим с людьми в серии публикаций, где я соберу всю информацию, которая потребуется вам, если вы только начинаете знакомство с нейронными сетями. В этой статье, я не буду делать сильный акцент на Java и буду объяснять все на примерах, чтобы вы сами смогли перенести это на любой, нужный вам язык программирования. В последующих статьях, я расскажу о своем приложении, написанном под андроид, которое предсказывает движение акций или валюты. Иными словами, всех желающих окунуться в мир нейронных сетей и жаждущих простого и доступного изложения информации или просто тех, кто что-то не понял и хочет подтянуть, добро пожаловать под кат.
Первым и самым важным моим открытием был плейлист американского программиста Джеффа Хитона, в котором он подробно и наглядно разбирает принципы работы нейронных сетей и их классификации. После просмотра этого плейлиста, я решил создать свою нейронную сеть, начав с самого простого примера. Вам наверняка известно, что когда ты только начинаешь учить новый язык, первой твоей программой будет Hello World. Это своего рода традиция. В мире машинного обучения тоже есть свой Hello world и это нейросеть решающая проблему исключающего или(XOR). Таблица исключающего или выглядит следующим образом:
| a | b | c |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Что такое нейронная сеть?
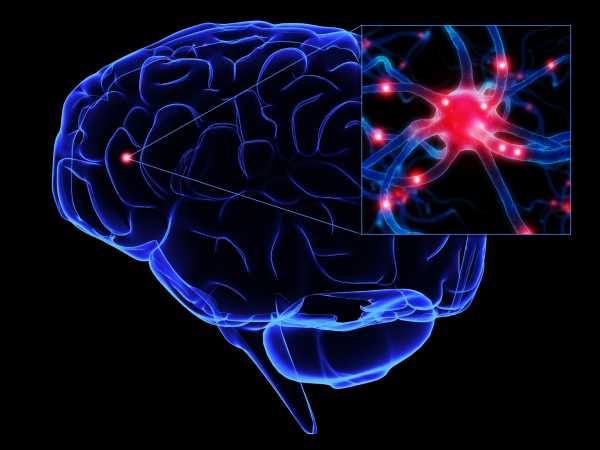
Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами. Структура нейронной сети пришла в мир программирования прямиком из биологии. Благодаря такой структуре, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Заинтересовавшимся обязательно к просмотру 2 видео из TED Talks: Видео 1, Видео 2). Другими словами, нейросеть это машинная интерпретация мозга человека, в котором находятся миллионы нейронов передающих информацию в виде электрических импульсов.
Какие бывают нейронные сети?
Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.
Для чего нужны нейронные сети?
Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:
Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.
Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.
Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.
Что такое нейрон?
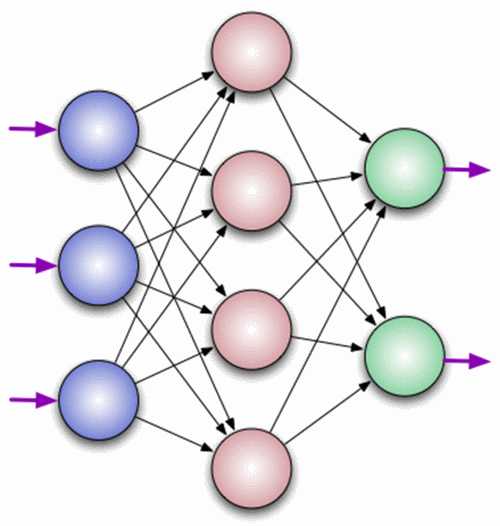
Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый). Также есть нейрон смещения и контекстный нейрон о которых мы поговорим в следующей статье. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат. У каждого из нейронов есть 2 основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.
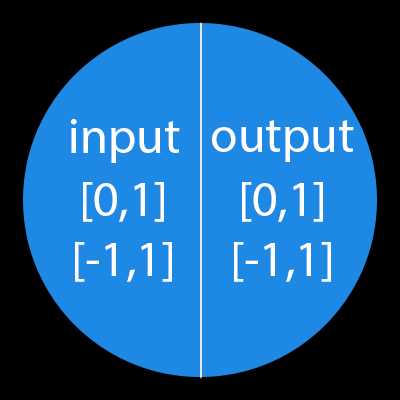
Важно помнить, что нейроны оперируют числами в диапазоне [0,1] или [-1,1]. А как же, вы спросите, тогда обрабатывать числа, которые выходят из данного диапазона? На данном этапе, самый простой ответ — это разделить 1 на это число. Этот процесс называется нормализацией, и он очень часто используется в нейронных сетях. Подробнее об этом чуть позже.
Что такое синапс?
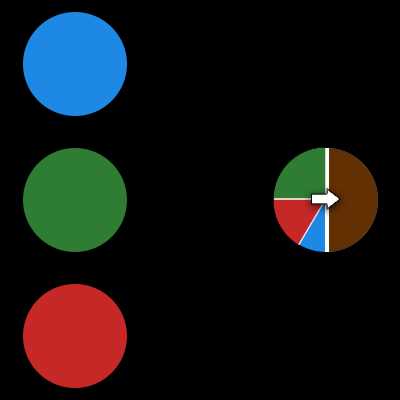
Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.
Как работает нейронная сеть?
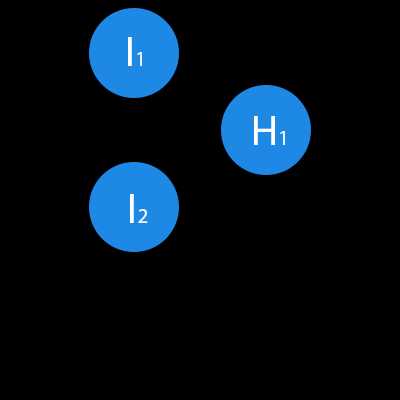
В данном примере изображена часть нейронной сети, где буквами I обозначены входные нейроны, буквой H — скрытый нейрон, а буквой w — веса. Из формулы видно, что входная информация — это сумма всех входных данных, умноженных на соответствующие им веса. Тогда дадим на вход 1 и 0. Пусть w1=0.4 и w2 = 0.7 Входные данные нейрона Н1 будут следующими: 1*0.4+0*0.7=0.4. Теперь когда у нас есть входные данные, мы можем получить выходные данные, подставив входное значение в функцию активации (подробнее о ней далее). Теперь, когда у нас есть выходные данные, мы передаем их дальше. И так, мы повторяем для всех слоев, пока не дойдем до выходного нейрона. Запустив такую сеть в первый раз мы увидим, что ответ далек от правильно, потому что сеть не натренирована. Чтобы улучшить результаты мы будем ее тренировать. Но прежде чем узнать как это делать, давайте введем несколько терминов и свойств нейронной сети.
Функция активации
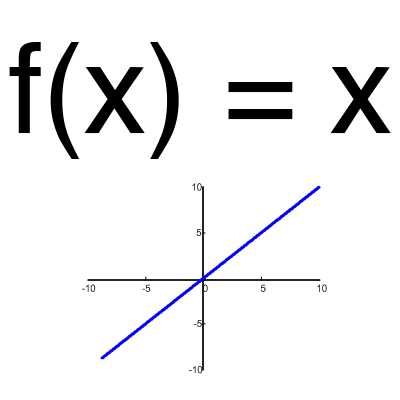
Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.
Сигмоид
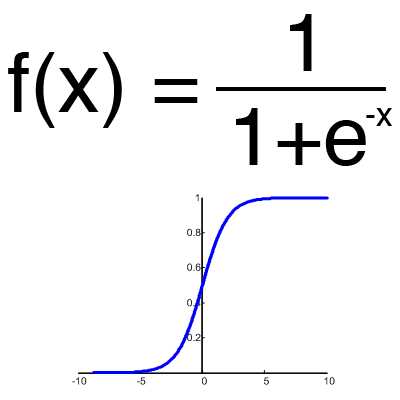
Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.
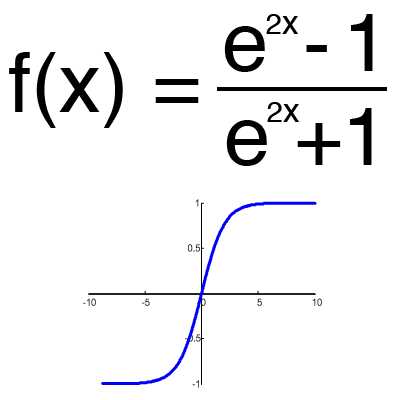
Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции [-1,1]. Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.
Тренировочный сет
Тренировочный сет — это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1,1xor1=0.
Итерация
Эпоха
При инициализации нейронной сети эта величина устанавливается в 0 и имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована сеть и соответственно, ее результат. Эпоха увеличивается каждый раз, когда мы проходим весь набор тренировочных сетов, в нашем случае, 4 сетов или 4 итераций.
раз увеличивается итерация, а потом уже эпоха и никак не наоборот. Другими словами, нельзя сначала тренировать нейросеть только на одном сете, потом на другом и тд. Нужно тренировать каждый сет один раз за эпоху. Так, вы сможете избежать ошибок в вычислениях.
Ошибка
Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка формируется каждую эпоху и должна идти на спад. Если этого не происходит, значит, вы что-то делаете не так. Ошибку можно вычислить разными путями, но мы рассмотрим лишь три основных способа: Mean Squared Error (далее MSE), Root MSE и Arctan. Здесь нет какого-либо ограничения на использование, как в функции активации, и вы вольны выбрать любой метод, который будет приносить вам наилучший результат. Стоит лишь учитывать, что каждый метод считает ошибки по разному. У Arctan, ошибка, почти всегда, будет больше, так как он работает по принципу: чем больше разница, тем больше ошибка. У Root MSE будет наименьшая ошибка, поэтому, чаще всего, используют MSE, которая сохраняет баланс в вычислении ошибки.
MSE
Root MSE
Arctan
Принцип подсчета ошибки во всех случаях одинаков. За каждый сет, мы считаем ошибку, отняв от идеального ответа, полученный. Далее, либо возводим в квадрат, либо вычисляем квадратный тангенс из этой разности, после чего полученное число делим на количество сетов.
Задача
Теперь, чтобы проверить себя, подсчитайте результат, данной нейронной сети, используя сигмоид, и ее ошибку, используя MSE.
Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.
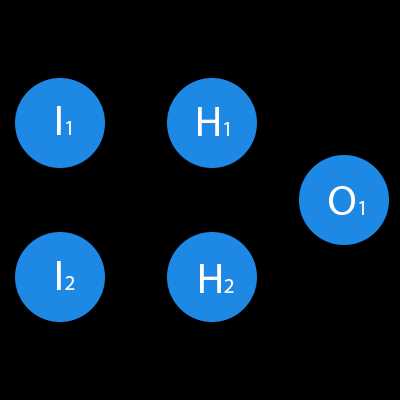
Решениеh2input = 1*0.45+0*-0.12=0.45
h2output = sigmoid(0.45)=0.61
h3input = 1*0.78+0*0.13=0.78
h3output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
O1ideal = 1 (0xor1=1)
Error = ((1-0.33)^2)/1=0.45
Результат — 0.33, ошибка — 45%.
Большое спасибо за внимание! Надеюсь, что данная статья смогла помочь вам в изучении нейронных сетей. В следующей статье, я расскажу о нейронах смещения и о том, как тренировать нейронную сеть, используя метод обратного распространения и градиентного спуска.
Использованные ресурсы:
— Раз
— Два
— Три
habr.com
3. Основы ИНС – Нейронные сети
В предыдущей главе мы ознакомились с такими понятиями, как искусственный интеллект, машинное обучение и искусственные нейронные сети.
В этой главе я детально опишу модель искусственного нейрона, расскажу о подходах к обучению сети, а также опишу некоторые известные виды искусственных нейронных сетей, которые мы будем изучать в следующих главах.
Упрощение
В прошлой главе я постоянно говорил о каких-то серьезных упрощениях. Причина упрощений заключается в том, что никакие современные компьютеры не могут быстро моделировать такие сложные системы, как наш мозг. К тому же, как я уже говорил, наш мозг переполнен различными биологическими механизмами, не относящиеся к обработке информации.
Нам нужна модель преобразования входного сигнала в нужный нам выходной. Все остальное нас не волнует. Начинаем упрощать.
Биологическая структура → схема
В предыдущей главе вы поняли, насколько сложно устроены биологические нейронные сети и биологические нейроны. Вместо изображения нейронов в виде чудовищ с щупальцами давайте просто будем рисовать схемы.
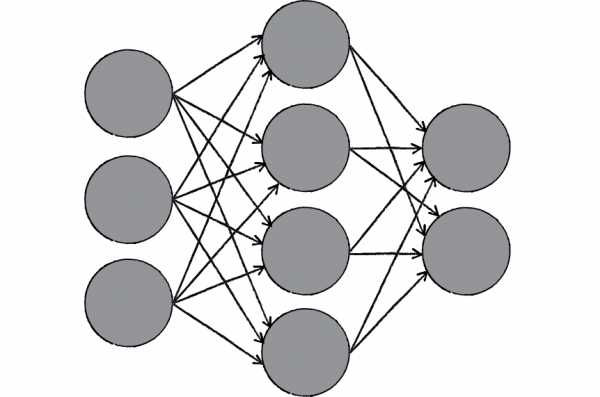
Вообще говоря, есть несколько способов графического изображения нейронных сетей и нейронов. Здесь мы будем изображать искусственные нейроны в виде кружков.
Вместо сложного переплетения входов и выходов будем использовать стрелки, обозначающие направление движения сигнала.
Таким образом искусственная нейронная сеть может быть представлена в виде совокупности кружков (искусственных нейронов), связанных стрелками.
Электрические сигналы → числа
В реальной биологической нейронной сети от входов сети к выходам передается электрический сигнал. В процессе прохода по нейронной сети он может изменяться.

Электрический сигнал всегда будет электрическим сигналом. Концептуально ничего не изменяется. Но что же тогда меняется? Меняется величина этого электрического сигнала (сильнее/слабее). А любую величину всегда можно выразить числом (больше/меньше).
В нашей модели искусственной нейронной сети нам совершенно не нужно реализовывать поведение электрического сигнала, так как от его реализации все равно ничего зависеть не будет.
На входы сети мы будем подавать какие-то числа, символизирующие величины электрического сигнала, если бы он был. Эти числа будут продвигаться по сети и каким-то образом меняться. На выходе сети мы получим какое-то результирующее число, являющееся откликом сети.
Для удобства все равно будем называть наши числа, циркулирующие в сети, сигналами.
Синапсы → веса связей
Вспомним картинку из первой главы, на которой цветом были изображены связи между нейронами – синапсы. Синапсы могут усиливать или ослаблять проходящий по ним электрический сигнал.
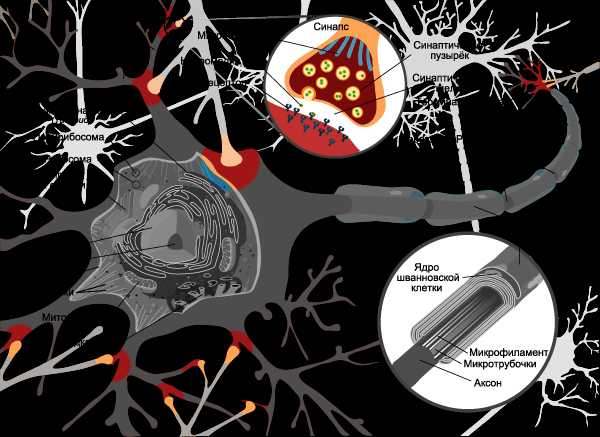
Давайте характеризовать каждую такую связь определенным числом, называемым весом данной связи. Сигнал, прошедший через данную связь, умножается на вес соответствующей связи.
Это ключевой момент в концепции искусственных нейронных сетей, я объясню его подробнее. Посмотрите на картинку ниже. Теперь каждой черной стрелке (связи) на этой картинке соответствует некоторое число \( w_i \) (вес связи). И когда сигнал проходит по этой связи, его величина умножается на вес этой связи.
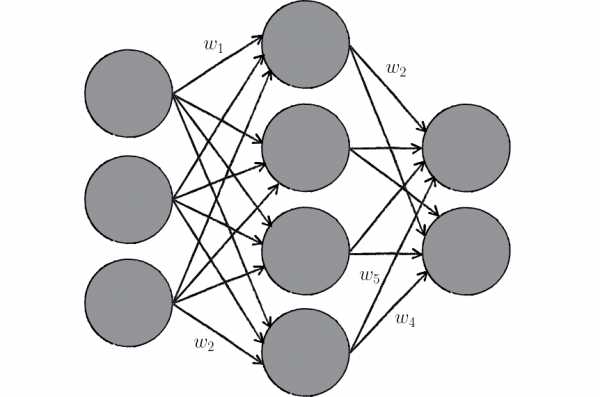
На приведенном выше рисунке вес стоит не у каждой связи лишь потому, что там нет места для обозначений. В реальности у каждой \( i \)-ой связи свой собственный \( w_i \)-ый вес.
Искусственный нейрон
Теперь мы переходим к рассмотрению внутренней структуры искусственного нейрона и того, как он преобразует поступающий на его входы сигнал.
На рисунке ниже представлена полная модель искусственного нейрона.

Не пугайтесь, ничего сложного здесь нет. Давайте рассмотрим все подробно слева направо.
Входы, веса и сумматор
У каждого нейрона, в том числе и у искусственного, должны быть какие-то входы, через которые он принимает сигнал. Мы уже вводили понятие весов, на которые умножаются сигналы, проходящие по связи. На картинке выше веса изображены кружками.
Поступившие на входы сигналы умножаются на свои веса. Сигнал первого входа \( x_1 \) умножается на соответствующий этому входу вес \( w_1 \). В итоге получаем \( x_1w_1 \). И так до \( n \)-ого входа. В итоге на последнем входе получаем \( x_nw_n \).
Теперь все произведения передаются в сумматор. Уже исходя из его названия можно понять, что он делает. Он просто суммирует все входные сигналы, умноженные на соответствующие веса:
\[ x_1w_1+x_2w_2+\cdots+x_nw_n = \sum\limits^n_{i=1}x_iw_i \]
Математическая справка
Сигма – ВикипедияКогда необходимо коротко записать большое выражение, состоящее из суммы повторяющихся/однотипных членов, то используют знак сигмы.
Рассмотрим простейший вариант записи:
\[ \sum\limits^5_{i=1}i=1+2+3+4+5 \]
Таким образом снизу сигмы мы присваиваем переменной-счетчику \( i \) стартовое значение, которое будет увеличиваться, пока не дойдет до верхней границы (в примере выше это 5).
Верхняя граница может быть и переменной. Приведу пример такого случая.
Пусть у нас есть \( n \) магазинов. У каждого магазина есть свой номер: от 1 до \( n \). Каждый магазин приносит прибыль. Возьмем какой-то (неважно, какой) \( i \)-ый магазин. Прибыль от него равна \( p_i \).
Если мы хотим посчитать общую прибыль от всех магазинов (обозначим ее за \( P \)), то нам пришлось бы писать длинную сумму:
\[ P = p_1+p_2+\cdots+p_i+\cdots+p_n \]
Как видно, все члены этой суммы однотипны. Тогда их можно коротко записать следующим образом:
\[ P=\sum\limits^n_{i=1}p_i \]
Словами: «Просуммируй прибыли всех магазинов, начиная с первого и заканчивая \( n \)-ым». В виде формулы это гораздо проще, удобнее и красивее.
Результатом работы сумматора является число, называемое взвешенной суммой.
Взвешенная сумма (Weighted sum) (\( net \)) — сумма входных сигналов, умноженных на соответствующие им веса.\[ net=\sum\limits^n_{i=1}x_iw_i \]
Роль сумматора очевидна – он агрегирует все входные сигналы (которых может быть много) в какое-то одно число – взвешенную сумму, которая характеризует поступивший на нейрон сигнал в целом. Еще взвешенную сумму можно представить как степень общего возбуждения нейрона.
Пример
Для понимания роли последнего компонента искусственного нейрона – функции активации – я приведу аналогию.
Давайте рассмотрим один искусственный нейрон. Его задача – решить, ехать ли отдыхать на море. Для этого на его входы мы подаем различные данные. Пусть у нашего нейрона будет 4 входа:
- Стоимость поездки
- Какая на море погода
- Текущая обстановка с работой
- Будет ли на пляже закусочная
Все эти параметры будем характеризовать 0 или 1. Соответственно, если погода на море хорошая, то на этот вход подаем 1. И так со всеми остальными параметрами.
Если у нейрона есть четыре входа, то должно быть и четыре весовых коэффициента. В нашем примере весовые коэффициенты можно представить как показатели важности каждого входа, влияющие на общее решение нейрона. Веса входов распределим следующим образом:
- 5
- 4
- 1
- 1
Нетрудно заметить, что очень большую роль играют факторы стоимости и погоды на море (первые два входа). Они же и будут играть решающую роль при принятии нейроном решения.
Пусть на входы нашего нейрона мы подаем следующие сигналы:
- 1
- 0
- 0
- 1
Умножаем веса входов на сигналы соответствующих входов:
- 5
- 0
- 0
- 1
Взвешенная сумма для такого набора входных сигналов равна 6:
\[ net=\sum\limits^4_{i=1}x_iw_i = 5 + 0 + 0 + 1 =6 \]
Все классно, но что делать дальше? Как нейрон должен решить, ехать на море или нет? Очевидно, нам нужно как-то преобразовать нашу взвешенную сумму и получить ответ.
Вот на сцену выходит функция активации.
Функция активации
Просто так подавать взвешенную сумму на выход достаточно бессмысленно. Нейрон должен как-то обработать ее и сформировать адекватный выходной сигнал. Именно для этих целей и используют функцию активации.
Она преобразует взвешенную сумму в какое-то число, которое и является выходом нейрона (выход нейрона обозначим переменной \( out \)).
Для разных типов искусственных нейронов используют самые разные функции активации. В общем случае их обозначают символом \( \phi(net) \). Указание взвешенного сигнала в скобках означает, что функция активации принимает взвешенную сумму как параметр.
Функция активации (Activation function) (\( \phi(net) \)) — функция, принимающая взвешенную сумму как аргумент. Значение этой функции и является выходом нейрона (\( out \)).\[ out=\phi(net) \]
Далее мы подробно рассмотрим самые известные функции активации.
Функция единичного скачка
Самый простой вид функции активации. Выход нейрона может быть равен только 0 или 1. Если взвешенная сумма больше определенного порога \( b \), то выход нейрона равен 1. Если ниже, то 0.
Как ее можно использовать? Предположим, что мы поедем на море только тогда, когда взвешенная сумма больше или равна 5. Значит наш порог равен 5:
\[ b=5 \]
В нашем примере взвешенная сумма равнялась 6, а значит выходной сигнал нашего нейрона равен 1. Итак, мы едем на море.
Однако если бы погода на море была бы плохой, а также поездка была бы очень дорогой, но имелась бы закусочная и обстановка с работой нормальная (входы: 0011), то взвешенная сумма равнялась бы 2, а значит выход нейрона равнялся бы 0. Итак, мы никуда не едем.
В общем, нейрон смотрит на взвешенную сумму и если она получается больше его порога, то нейрон выдает выходной сигнал, равный 1.
Графически эту функцию активации можно изобразить следующим образом.
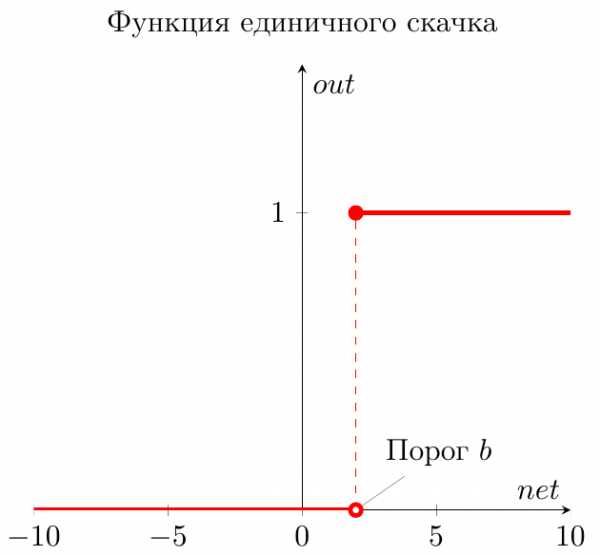
На горизонтальной оси расположены величины взвешенной суммы. На вертикальной оси — значения выходного сигнала. Как легко видеть, возможны только два значения выходного сигнала: 0 или 1. Причем 0 будет выдаваться всегда от минус бесконечности и вплоть до некоторого значения взвешенной суммы, называемого порогом. Если взвешенная сумма равна порогу или больше него, то функция выдает 1. Все предельно просто.
Теперь запишем эту функцию активации математически. Почти наверняка вы сталкивались с таким понятием, как составная функция. Это когда мы под одной функцией объединяем несколько правил, по которым рассчитывается ее значение. В виде составной функции функция единичного скачка будет выглядеть следующим образом:
\[ out(net) = \begin{cases} 0, net < b \\ 1, net \geq b \end{cases} \]
В этой записи нет ничего сложного. Выход нейрона (\( out \)) зависит от взвешенной суммы (\( net \)) следующим образом: если \( net \) (взвешенная сумма) меньше какого-то порога (\( b \)), то \( out \) (выход нейрона) равен 0. А если \( net \) больше или равен порогу \( b \), то \( out \) равен 1.
Сигмоидальная функция
На самом деле существует целое семейство сигмоидальных функций, некоторые из которых применяют в качестве функции активации в искусственных нейронах.
Все эти функции обладают некоторыми очень полезными свойствами, ради которых их и применяют в нейронных сетях. Эти свойства станут очевидными после того, как вы увидите графики этих функций.
Итак… самая часто используемая в нейронных сетях сигмоида — логистическая функция.
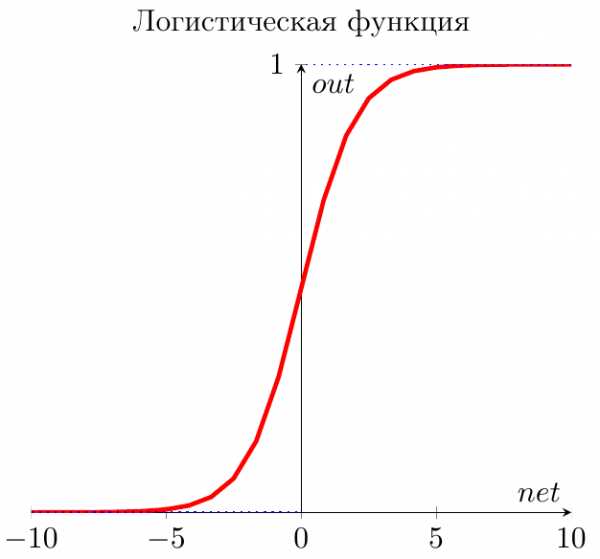
График этой функции выглядит достаточно просто. Если присмотреться, то можно увидеть некоторое подобие английской буквы \( S \), откуда и пошло название семейства этих функций.
А вот так она записывается аналитически:
\[ out(net)=\frac{1}{1+\exp(-a \cdot net)} \]
Что за параметр \( a \)? Это какое-то число, которое характеризует степень крутизны функции. Ниже представлены логистические функции с разным параметром \( a \).
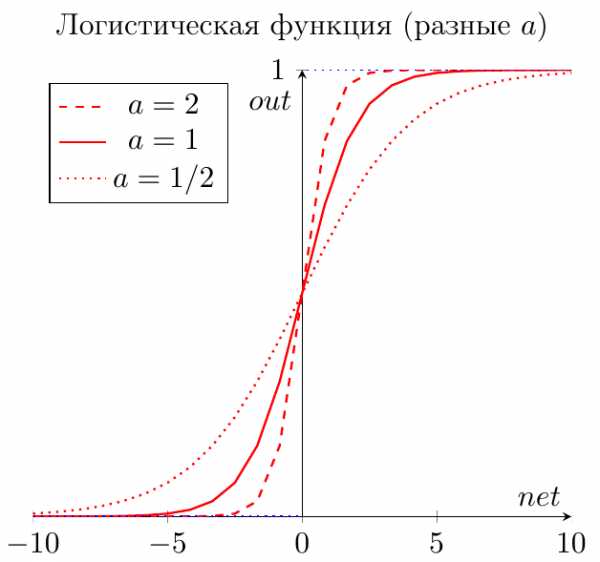
Вспомним наш искусственный нейрон, определяющий, надо ли ехать на море. В случае с функцией единичного скачка все было очевидно. Мы либо едем на море (1), либо нет (0).
Здесь же случай более приближенный к реальности. Мы до конца полностью не уверены (в особенности, если вы параноик) – стоит ли ехать? Тогда использование логистической функции в качестве функции активации приведет к тому, что вы будете получать цифру между 0 и 1. Причем чем больше взвешенная сумма, тем ближе выход будет к 1 (но никогда не будет точно ей равен). И наоборот, чем меньше взвешенная сумма, тем ближе выход нейрона будет к 0.
Например, выход нашего нейрона равен 0.8. Это значит, что он считает, что поехать на море все-таки стоит. Если бы его выход был бы равен 0.2, то это означает, что он почти наверняка против поездки на море.
Какие же замечательные свойства имеет логистическая функция?
- она является «сжимающей» функцией, то есть вне зависимости от аргумента (взвешенной суммы), выходной сигнал всегда будет в пределах от 0 до 1
- она более гибкая, чем функция единичного скачка – ее результатом может быть не только 0 и 1, но и любое число между ними
- во всех точках она имеет производную, и эта производная может быть выражена через эту же функцию
Именно из-за этих свойств логистическая функция чаще всего используются в качестве функции активации в искусственных нейронах.
Гиперболический тангенс
Однако есть и еще одна сигмоида – гиперболический тангенс. Он применяется в качестве функции активации биологами для более реалистичной модели нервной клетки.
Такая функция позволяет получить на выходе значения разных знаков (например, от -1 до 1), что может быть полезным для ряда сетей.
Функция записывается следующим образом:
\[ out(net) = \tanh\left(\frac{net}{a}\right) \]
В данной выше формуле параметр \( a \) также определяет степень крутизны графика этой функции.
А вот так выглядит график этой функции.
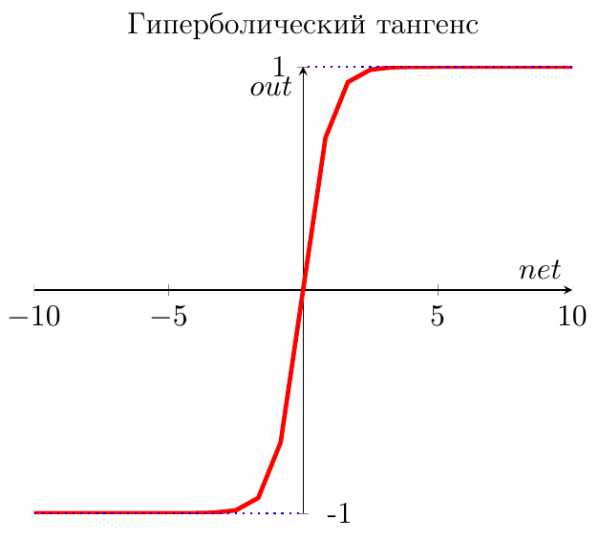
Как видите, он похож на график логистической функции. Гиперболический тангенс обладает всеми полезными свойствами, которые имеет и логистическая функция.
Что мы узнали?
Теперь вы получили полное представление о внутренней структуре искусственного нейрона. Я еще раз приведу краткое описание его работы.
У нейрона есть входы. На них подаются сигналы в виде чисел. Каждый вход имеет свой вес (тоже число). Сигналы на входе умножаются на соответствующие веса. Получаем набор «взвешенных» входных сигналов.
Далее этот набор попадает в сумматор, которой просто складывает все входные сигналы, помноженные на веса. Получившееся число называют взвешенной суммой.
Затем взвешенная сумма преобразуется функцией активации и мы получаем выход нейрона.
Сформулируем теперь самое короткое описание работы нейрона – его математическую модель:
Математическая модель искусственного нейрона с \( n \) входами:\[ out=\phi\left(\sum\limits^n_{i=1}x_iw_i\right) \]
где
\( \phi \) – функция активации
\( \sum\limits^n_{i=1}x_iw_i \) – взвешенная сумма, как сумма \( n \) произведений входных сигналов на соответствующие веса.
Виды ИНС
Мы разобрались со структурой искусственного нейрона. Искусственные нейронные сети состоят из совокупности искусственных нейронов. Возникает логичный вопрос – а как располагать/соединять друг с другом эти самые искусственные нейроны?
Как правило, в большинстве нейронных сетей есть так называемый входной слой, который выполняет только одну задачу – распределение входных сигналов остальным нейронам. Нейроны этого слоя не производят никаких вычислений.
А дальше начинаются различия…
Однослойные нейронные сети
В однослойных нейронных сетях сигналы с входного слоя сразу подаются на выходной слой. Он производит необходимые вычисления, результаты которых сразу подаются на выходы.
Выглядит однослойная нейронная сеть следующим образом:
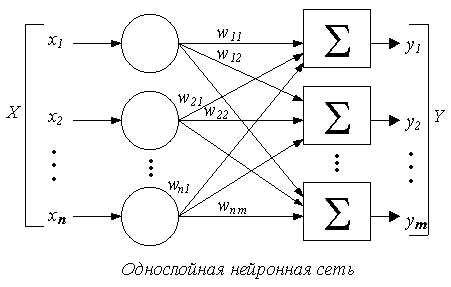
На этой картинке входной слой обозначен кружками (он не считается за слой нейронной сети), а справа расположен слой обычных нейронов.
Нейроны соединены друг с другом стрелками. Над стрелками расположены веса соответствующих связей (весовые коэффициенты).
Однослойная нейронная сеть (Single-layer neural network) — сеть, в которой сигналы от входного слоя сразу подаются на выходной слой, который и преобразует сигнал и сразу же выдает ответ.
Многослойные нейронные сети
Такие сети, помимо входного и выходного слоев нейронов, характеризуются еще и скрытым слоем (слоями). Понять их расположение просто – эти слои находятся между входным и выходным слоями.

Такая структура нейронных сетей копирует многослойную структуру определенных отделов мозга.
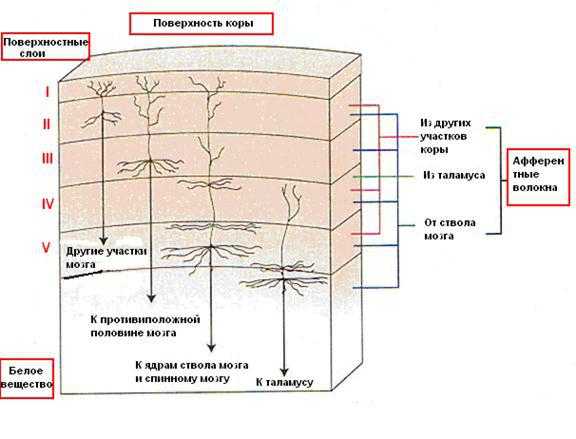
Название скрытый слой получил неслучайно. Дело в том, что только относительно недавно были разработаны методы обучения нейронов скрытого слоя. До этого обходились только однослойными нейросетями.
Многослойные нейронные сети обладают гораздо большими возможностями, чем однослойные.
Работу скрытых слоев нейронов можно сравнить с работой большого завода. Продукт (выходной сигнал) на заводе собирается по стадиям. После каждого станка получается какой-то промежуточный результат. Скрытые слои тоже преобразуют входные сигналы в некоторые промежуточные результаты.
Многослойная нейронная сеть (Multilayer neural network) — нейронная сеть, состоящая из входного, выходного и расположенного(ых) между ними одного (нескольких) скрытых слоев нейронов.
Сети прямого распространения
Можно заметить одну очень интересную деталь на картинках нейросетей в примерах выше.
Во всех примерах стрелки строго идут слева направо, то есть сигнал в таких сетях идет строго от входного слоя к выходному.
Сети прямого распространения (Feedforward neural network) (feedforward сети) — искусственные нейронные сети, в которых сигнал распространяется строго от входного слоя к выходному. В обратном направлении сигнал не распространяется.
Такие сети широко используются и вполне успешно решают определенный класс задач: прогнозирование, кластеризация и распознавание.
Однако никто не запрещает сигналу идти и в обратную сторону.
Сети с обратными связями
В сетях такого типа сигнал может идти и в обратную сторону. В чем преимущество?
Дело в том, что в сетях прямого распространения выход сети определяется входным сигналом и весовыми коэффициентами при искусственных нейронах.
А в сетях с обратными связями выходы нейронов могут возвращаться на входы. Это означает, что выход какого-нибудь нейрона определяется не только его весами и входным сигналом, но еще и предыдущими выходами (так как они снова вернулись на входы).
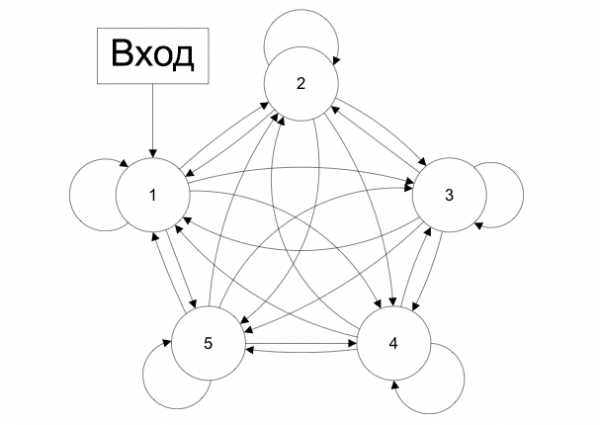
Возможность сигналов циркулировать в сети открывает новые, удивительные возможности нейронных сетей. С помощью таких сетей можно создавать нейросети, восстанавливающие или дополняющие сигналы. Другими словами такие нейросети имеют свойства кратковременной памяти (как у человека).
Сети с обратными связями (Recurrent neural network) — искусственные нейронные сети, в которых выход нейрона может вновь подаваться на его вход. В более общем случае это означает возможность распространения сигнала от выходов к входам.
Обучение нейронной сети
Теперь давайте чуть более подробно рассмотрим вопрос обучения нейронной сети. Что это такое? И каким образом это происходит?
Что такое обучение сети?
Искусственная нейронная сеть – это совокупность искусственных нейронов. Теперь давайте возьмем, например, 100 нейронов и соединим их друг с другом. Ясно, что при подаче сигнала на вход, мы получим что-то бессмысленное на выходе.
Значит нам надо менять какие-то параметры сети до тех пор, пока входной сигнал не преобразуется в нужный нам выходной.
Что мы можем менять в нейронной сети?
Изменять общее количество искусственных нейронов бессмысленно по двум причинам. Во-первых, увеличение количества вычислительных элементов в целом лишь делает систему тяжеловеснее и избыточнее. Во-вторых, если вы соберете 1000 дураков вместо 100, то они все-равно не смогут правильно ответить на вопрос.
Сумматор изменить не получится, так как он выполняет одну жестко заданную функцию – складывать. Если мы его заменим на что-то или вообще уберем, то это вообще уже не будет искусственным нейроном.
Если менять у каждого нейрона функцию активации, то мы получим слишком разношерстную и неконтролируемую нейронную сеть. К тому же, в большинстве случаев нейроны в нейронных сетях одного типа. То есть они все имеют одну и ту же функцию активации.
Остается только один вариант – менять веса связей.
Обучение нейронной сети (Training) — поиск такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной.
Такой подход к термину «обучение нейронной сети» соответствует и биологическим нейросетям. Наш мозг состоит из огромного количества связанных друг с другом нейросетей. Каждая из них в отдельности состоит из нейронов одного типа (функция активации одинаковая). Мы обучаемся благодаря изменению синапсов – элементов, которые усиливают/ослабляют входной сигнал.
Однако есть еще один важный момент. Если обучать сеть, используя только один входной сигнал, то сеть просто «запомнит правильный ответ». Со стороны будет казаться, что она очень быстро «обучилась». И как только вы подадите немного измененный сигнал, ожидая увидеть правильный ответ, то сеть выдаст бессмыслицу.
В самом деле, зачем нам сеть, определяющая лицо только на одном фото. Мы ждем от сети способности обобщать какие-то признаки и узнавать лица и на других фотографиях тоже.
Именно с этой целью и создаются обучающие выборки.
Обучающая выборка (Training set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит обучение сети.
После обучения сети, то есть когда сеть выдает корректные результаты для всех входных сигналов из обучающей выборки, ее можно использовать на практике.
Однако прежде чем пускать свежеиспеченную нейросеть в бой, часто производят оценку качества ее работы на так называемой тестовой выборке.
Тестовая выборка (Testing set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит оценка качества работы сети.
Мы поняли, что такое «обучение сети» – подбор правильного набора весов. Теперь возникает вопрос – а как можно обучать сеть? В самом общем случае есть два подхода, приводящие к разным результатам: обучение с учителем и обучение без учителя.
Обучение с учителем
Суть данного подхода заключается в том, что вы даете на вход сигнал, смотрите на ответ сети, а затем сравниваете его с уже готовым, правильным ответом.
Важный момент. Не путайте правильные ответы и известный алгоритм решения! Вы можете обвести пальцем лицо на фото (правильный ответ), но не сможете сказать, как это сделали (известный алгоритм). Тут такая же ситуация.
Затем, с помощью специальных алгоритмов, вы меняете веса связей нейронной сети и снова даете ей входной сигнал. Сравниваете ее ответ с правильным и повторяете этот процесс до тех пор, пока сеть не начнет отвечать с приемлемой точностью (как я говорил в 1 главе, однозначно точных ответов сеть давать не может).
Обучение с учителем (Supervised learning) — вид обучения сети, при котором ее веса меняются так, чтобы ответы сети минимально отличались от уже готовых правильных ответов.
Где взять правильные ответы?
Если мы хотим, чтобы сеть узнавала лица, мы можем создать обучающую выборку на 1000 фотографий (входные сигналы) и самостоятельно выделить на ней лица (правильные ответы).
Если мы хотим, чтобы сеть прогнозировала рост/падение цен, то обучающую выборку надо делать, основываясь на прошлых данных. В качестве входных сигналов можно брать определенные дни, общее состояние рынка и другие параметры. А в качестве правильных ответов – рост и падение цены в те дни.
И так далее…
Стоит отметить, что учитель, конечно же, не обязательно человек. Дело в том, что порой сеть приходится тренировать часами и днями, совершая тысячи и десятки тысяч попыток. В 99% случаев эту роль выполняет компьютер, а точнее, специальная компьютерная программа.
Обучение без учителя
Обучение без учителя применяют тогда, когда у нас нет правильных ответов на входные сигналы. В этом случае вся обучающая выборка состоит из набора входных сигналов.
Что же происходит при таком обучении сети? Оказывается, что при таком «обучении» сеть начинает выделять классы подаваемых на вход сигналов. Короче говоря – сеть начинает кластеризацию.
Например, вы демонстрируете сети конфеты, пирожные и торты. Вы никак не регулируете работу сети. Вы просто подаете на ее входы данные о данном объекте. Со временем сеть начнет выдавать сигналы трех разных типов, которые и отвечают за объекты на входе.
Обучение без учителя (Unsupervised learning) — вид обучения сети, при котором сеть самостоятельно классифицирует входные сигналы. Правильные (эталонные) выходные сигналы не демонстрируются.
Выводы
В этой главе вы узнали все о структуре искусственного нейрона, а также получили полное представление о том, как он работает (и о его математической модели).
Более того, вы теперь знаете о различных видах искусственных нейронных сетей: однослойные, многослойные, а также feedforward сети и сети с обратными связями.
Вы также ознакомились с тем, что представляет собой обучение сети с учителем и без учителя.
Вы уже знаете необходимую теорию. Последующие главы – рассмотрение конкретных видов нейронных сетей, конкретные алгоритмы их обучения и практика программирования.
Вопросы и задачи
Материал этой главы надо знать очень хорошо, так как в ней содержатся основные теоретические сведения по искусственным нейронным сетям. Обязательно добейтесь уверенных и правильных ответов на все нижеприведенные вопросы и задачи.
Опишите упрощения ИНС по сравнению с биологическими нейросетями.
1. Сложную и запутанную структуру биологических нейронных сетей упрощают и представляют в виде схем. Оставляют только модель обработки сигнала.2. Природа электрических сигналов в нейронных сетях одна и та же. Разница только в их величине. Убираем электрические сигналы, а вместо них используем числа, обозначающие величину проходящего сигнала.
3. Синапсы упрощаем до обычных чисел (весов связей), характеризующих связи между нейронами. Проходящий по связи сигнал просто умножается на вес этой связи.
Из каких элементов состоит искусственный нейрон?
Искусственный нейрон состоит из входов, весовых коэффициентов, соответствующих этим входам, сумматора и функции активации.
Что такое взвешенная сумма? Какой компонент искусственного нейрона ее вычисляет?
Взвешенной суммой называют сумму всех входов, умноженных на соответствующие весовые коэффициенты. Обычно ее обозначают за \( net \).Взвешенную сумму вычисляет сумматор искусственного нейрона.

Вычислите взвешенную сумму нейрона (рисунок выше)
У данного нейрона 4 входа и 4 весовых коэффициента. Используем формулу расчета взвешенной суммы:\[ \sum\limits^4_{i=1}x_iw_i = 2 \cdot 0.5 + (-3) \cdot 2 + 1 \cdot 4 + 5 \cdot (-1) = -6 \]
Значит \( net=-6 \)
Что такое функция активации?
Функция активации – функция, преобразующая взвешенную сумму в выходной сигнал нейрона. Для разных целей используют разные функции активации, но чаще всего: функцию единичного скачка и различные сигмоиды.Функцию активации часто обозначают за \( \phi(net) \).
Запишите математическую модель искусственного нейрона.
Искусственный нейрон c \( n \) входами преобразовывает входной сигнал (число) в выходной сигнал (число) следующим образом:\[ out=\phi\left(\sum\limits^n_{i=1}x_iw_i\right) \]
Чем отличаются однослойные и многослойные нейронные сети?
Однослойные нейронные сети состоят из одного вычислительного слоя нейронов. Входной слой подает сигналы сразу на выходной слой, который и преобразует сигнал, и сразу выдает результат.Многослойные нейронные сети, помимо входного и выходного слоев, имеют еще и скрытые слои. Эти скрытые слои проводят какие-то внутренние промежуточные преобразования, наподобие этапов производства продуктов на заводе.
В чем отличие feedforward сетей от сетей с обратными связями?
Сети прямого распространения (feedforward сети) допускают прохождение сигнала только в одном направлении – от входов к выходам. Сети с обратными связями данных ограничений не имеют, и выходы нейронов могут вновь подаваться на входы.
Что такое обучающая выборка? В чем ее смысл?
Перед тем, как использовать сеть на практике (например, для решения текущих задач, ответов на которые у вас нет), необходимо собрать коллекцию задач с готовыми ответами, на которой и тренировать сеть. Это коллекция и называется обучающей выборкой.Если собрать слишком маленький набор входных и выходных сигналов, то сеть просто запомнит ответы и цель обучения не будет достигнута.
Что понимают под обучением сети?
Под обучением сети понимают процесс изменения весовых коэффициентов искусственных нейронов сети с целью подобрать такую их комбинацию, которая преобразует входной сигнал в корректный выходной.
Что такое обучение с учителем и без него?
При обучении сети с учителем ей на входы подают сигналы, а затем сравнивают ее выход с заранее известным правильным выходом. Этот процесс повторяют до тех пор, пока не будет достигнута необходимая точность ответов.Если сети только подают входные сигналы, без сравнения их с готовыми выходами, то сеть начинает самостоятельную классификацию этих входных сигналов. Другими словами она выполняет кластеризацию входных сигналов. Такое обучение называют обучением без учителя.
neuralnet.info
Нейросети: что это такое и как работает | Будущее
За последнюю пару лет искусственный интеллект незаметно отряхнулся от тегов «фантастика» и «геймдизайн» и прочно прописался в ежедневных новостных лентах. Сущности под таинственным названием «нейросети» опознают людей по фотографиям, водят автомобили, играют в покер и совершают научные открытия. При этом из новостей не всегда понятно, что же такое эти загадочные нейросети: сложные программы, особые компьютеры или стойки со стройными рядами серверов?
Конечно, уже из названия можно догадаться, что в нейросетях разработчики попытались скопировать устройство человеческого мозга: как известно, он состоит из множества простых клеток-нейронов, которые обмениваются друг с другом электрическими сигналами. Но чем тогда нейросети отличаются от обычного компьютера, который тоже собран из примитивных электрических деталей? И почему до современного подхода не додумались ещё полвека назад?
Давайте попробуем разобраться, что же кроется за словом «нейросети», откуда они взялись — и правда ли, что компьютеры прямо на наших глазах постепенно обретают разум.
Идея нейросети заключается в том, чтобы собрать сложную структуру из очень простых элементов. Вряд ли можно считать разумным один-единственный участок мозга — а вот люди обычно на удивление неплохо проходят тест на IQ. Тем не менее до сих пор идею создания разума «из ничего» обычно высмеивали: шутке про тысячу обезьян с печатными машинками уже сотня лет, а при желании критику нейросетей можно найти даже у Цицерона, который ехидно предлагал до посинения подбрасывать в воздух жетоны с буквами, чтобы рано или поздно получился осмысленный текст. Однако в XXI веке оказалось, что классики ехидничали зря: именно армия обезьян с жетонами может при должном упорстве захватить мир.
Красота начинается, когда нейронов много
На самом деле нейросеть можно собрать даже из спичечных коробков: это просто набор нехитрых правил, по которым обрабатывается информация. «Искусственным нейроном», или перцептроном, называется не какой-то особый прибор, а всего лишь несколько арифметических действий.
Работает перцептрон проще некуда: он получает несколько исходных чисел, умножает каждое на «ценность» этого числа (о ней чуть ниже), складывает и в зависимости от результата выдаёт 1 или –1. Например, мы фотографируем чистое поле и показываем нашему нейрону какую-нибудь точку на этой картинке — то есть посылаем ему в качестве двух сигналов случайные координаты. А затем спрашиваем: «Дорогой нейрон, здесь небо или земля?» — «Минус один, — отвечает болванчик, безмятежно разглядывая кучевое облако. — Ясно же, что земля».
«Тыкать пальцем в небо» — это и есть основное занятие перцептрона. Никакой точности от него ждать не приходится: с тем же успехом можно подбросить монетку. Магия начинается на следующей стадии, которая называется машинным обучением. Мы ведь знаем правильный ответ — а значит, можем записать его в свою программу. Вот и получается, что за каждую неверную догадку перцептрон в буквальном смысле получает штраф, а за верную — премию: «ценность» входящих сигналов вырастает или уменьшается. После этого программа прогоняется уже по новой формуле. Рано или поздно нейрон неизбежно «поймёт», что земля на фотографии снизу, а небо сверху, — то есть попросту начнёт игнорировать сигнал от того канала, по которому ему передают x-координаты. Если такому умудрённому опытом роботу подсунуть другую фотографию, то линию горизонта он, может, и не найдёт, но верх с низом уже точно не перепутает.
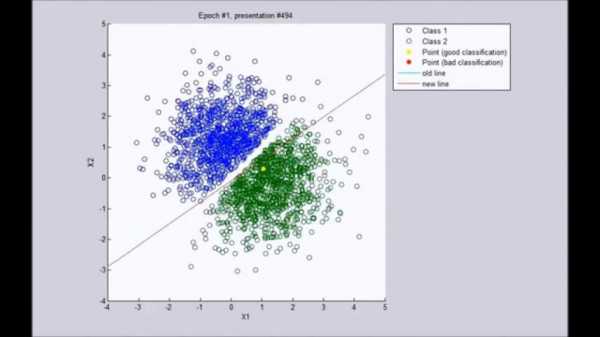
Чтобы нарисовать прямую линию, нейрон исчеркает весь лист
В реальной работе формулы немного сложнее, но принцип остаётся тем же. Перцептрон умеет выполнять только одну задачу: брать числа и раскладывать по двум стопкам. Самое интересное начинается тогда, когда таких элементов несколько, ведь входящие числа могут быть сигналами от других «кирпичиков»! Скажем, один нейрон будет пытаться отличить синие пиксели от зелёных, второй продолжит возиться с координатами, а третий попробует рассудить, у кого из этих двоих результаты ближе к истине. Если же натравить на синие пиксели сразу несколько нейронов и суммировать их результаты, то получится уже целый слой, в котором «лучшие ученики» будут получать дополнительные премии. Таким образом достаточно развесистая сеть может перелопатить целую гору данных и учесть при этом все свои ошибки.
Перцептроны устроены не намного сложнее, чем любые другие элементы компьютера, которые обмениваются единицами и нулями. Неудивительно, что первый прибор, устроенный по принципу нейросети — Mark I Perceptron, — появился уже в 1958 году, всего через десятилетие после первых компьютеров. Как было заведено в ту эпоху, нейроны у этого громоздкого устройства состояли не из строчек кода, а из радиоламп и резисторов. Учёный Фрэнк Розенблатт смог соорудить только два слоя нейросети, а сигналы на «Марк-1» подавались с импровизированного экрана размером в целых 400 точек. Устройство довольно быстро научилось распознавать простые геометрические формы — а значит, рано или поздно подобный компьютер можно было обучить, например, чтению букв.
Розенблатт и его перцептрон
Розенблатт был пламенным энтузиастом своего дела: он прекрасно разбирался в нейрофизиологии и вёл в Корнеллском университете популярнейший курс лекций, на котором подробно объяснял всем желающим, как с помощью техники воспроизводить принципы работы мозга. Учёный надеялся, что уже через несколько лет перцептроны превратятся в полноценных разумных роботов: они смогут ходить, разговаривать, создавать себе подобных и даже колонизировать другие планеты. Энтузиазм Розенблатта вполне можно понять: тогда учёные ещё верили, что для создания ИИ достаточно воспроизвести на компьютере полный набор операций математической логики. Тьюринг уже предложил свой знаменитый тест, Айзек Азимов призывал задуматься о необходимости законов роботехники, а освоение Вселенной казалось делом недалёкого будущего.
Впрочем, были среди пионеров кибернетики и неисправимые скептики, самым грозным из которых оказался бывший однокурсник Розенблатта, Марвин Минский. Этот учёный обладал не менее громкой репутацией: тот же Азимов отзывался о нём с неизменным уважением, а Стэнли Кубрик приглашал в качестве консультанта на съёмки «Космической одиссеи 2001 года». Даже по работе Кубрика видно, что на самом деле Минский ничего не имел против нейросетей: HAL 9000 состоит именно из отдельных логических узлов, которые работают в связке друг с другом. Минский и сам увлекался машинным обучением ещё в 1950-х. Просто Марвин непримиримо относился к научным ошибкам и беспочвенным надеждам: недаром именно в его честь Дуглас Адамс назвал своего андроида-пессимиста.

В отличие от Розенблатта, Минский дожил до триумфа ИИ
Сомнения скептиков того времени Минский подытожил в книге «Перцептрон» (1969), которая надолго отбила у научного сообщества интерес к нейросетям. Минский математически доказал, что у «Марка-1» есть два серьёзных изъяна. Во-первых, сеть всего с двумя слоями почти ничего не умела — а ведь это и так уже был огромный шкаф, пожирающий уйму электричества. Во-вторых, для многослойных сетей алгоритмы Розенблатта не годились: по его формуле часть сведений об ошибках сети могла потеряться, так и не дойдя до нужного слоя.
Минский не собирался сильно критиковать коллегу: он просто честно отметил сильные и слабые стороны его проекта, а сам продолжил заниматься своими разработками. Увы, в 1971 году Розенблатт погиб — исправлять ошибки перцептрона оказалось некому. «Обычные» компьютеры в 1970-х развивались семимильными шагами, поэтому после книги Минского исследователи попросту махнули рукой на искусственные нейроны и занялись более перспективными направлениями.
Развитие нейросетей остановилось на десять с лишним лет — сейчас эти годы называют «зимой искусственного интеллекта». К началу эпохи киберпанка математики наконец-то придумали более подходящие формулы для расчёта ошибок, но научное сообщество поначалу не обратило внимания на эти исследования. Только в 1986 году, когда уже третья подряд группа учёных независимо от других решила обнаруженную Минским проблему обучения многослойных сетей, работа над искусственным интеллектом наконец-то закипела с новой силой.
Хотя правила работы остались прежними, вывеска сменилась: теперь речь шла уже не о «перцептронах», а о «когнитивных вычислениях». Экспериментальных приборов никто уже не строил: теперь все нужные формулы проще было записать в виде несложного кода на обычном компьютере, а потом зациклить программу. Буквально за пару лет нейроны научились собирать в сложные структуры. Например, некоторые слои искали на изображении конкретные геометрические фигуры, а другие суммировали полученные данные. Именно так удалось научить компьютеры читать человеческий почерк. Вскоре стали появляться даже самообучающиеся сети, которые не получали «правильные ответы» от людей, а находили их сами. Нейросети сразу начали использовать и на практике: программу, которая распознавала цифры на чеках, с удовольствием взяли на вооружение американские банки.

1993 год: капча уже морально устарела
К середине 1990-х исследователи сошлись на том, что самое полезное свойство нейросетей — их способность самостоятельно придумывать верные решения. Метод проб и ошибок позволяет программе самой выработать для себя правила поведения. Именно тогда стали входить в моду соревнования самодельных роботов, которых программировали и обучали конструкторы-энтузиасты. А в 1997 году суперкомпьютер Deep Blue потряс любителей шахмат, обыграв чемпиона мира Гарри Каспарова.

Строго говоря, Deep Blue не учился на своих ошибках, а попросту перебирал миллионы комбинаций
Увы, примерно в те же годы нейросети упёрлись в потолок возможностей. Другие области программирования не стояли на месте — вскоре оказалось, что с теми же задачами куда проще справляются обычные продуманные и оптимизированные алгоритмы. Автоматическое распознавание текста сильно упростило жизнь работникам архивов и интернет-пиратам, роботы продолжали умнеть, но разговоры об искусственном интеллекте потихоньку заглохли. Для действительно сложных задач нейросетям по-прежнему не хватало вычислительной мощности.
Вторая «оттепель» ИИ случилась, только когда изменилась сама философия программирования.
В последнее десятилетие программисты — да и простые пользователи — часто жалуются, что никто больше не обращает внимания на оптимизацию. Раньше код сокращали как могли — лишь бы программа работала быстрее и занимала меньше памяти. Теперь даже простейший интернет-сайт норовит подгрести под себя всю память и обвешаться «библиотеками» для красивой анимации.
Конечно, для обычных программ это серьёзная проблема, — но как раз такого изобилия и не хватало нейросетям! Учёным давно известно, что если не экономить ресурсы, самые сложные задачи начинают решаться словно бы сами собой. Ведь именно так действуют все законы природы, от квантовой физики до эволюции: если повторять раз за разом бесчисленные случайные события, отбирая самые стабильные варианты, то из хаоса родится стройная и упорядоченная система. Теперь в руках человечества наконец-то оказался инструмент, который позволяет не ждать изменений миллиарды лет, а обучать сложные системы буквально на ходу.
В последние годы никакой революции в программировании не случилось — просто компьютеры накопили столько вычислительной мощности, что теперь любой ноутбук может взять сотню нейронов и прогнать каждый из них через миллион циклов обучения. Оказалось, что тысяче обезьян с пишущими машинками просто нужен очень терпеливый надсмотрщик, который будет выдавать им бананы за правильно напечатанные буквы, — тогда зверушки не только скопируют «Войну и мир», но и напишут пару новых романов не хуже.
Так и произошло третье пришествие перцептронов — на этот раз уже под знакомыми нам названиями «нейросети» и «глубинное обучение». Неудивительно, что новостями об успехах ИИ чаще всего делятся такие крупные корпорации как Google и IBM. Их главный ресурс — огромные дата-центры, где на мощных серверах можно тренировать многослойные нейросети. Эпоха машинного обучения по-настоящему началась именно сейчас, потому что в интернете и соцсетях наконец-то накопились те самые big data, то есть гигантские массивы информации, которые и скармливают нейросетям для обучения.
В итоге современные сети занимаются теми трудоёмкими задачами, на которые людям попросту не хватило бы жизни. Например, для поиска новых лекарств учёным до сих пор приходилось долго высчитывать, какие химические соединения стоит протестировать. А сейчас существует нейросеть, которая попросту перебирает все возможные комбинации веществ и предлагает наиболее перспективные направления исследований. Компьютер IBM Watson успешно помогает врачам в диагностике: обучившись на историях болезней, он легко находит в данных новых пациентов неочевидные закономерности.

Люди классифицируют информацию с помощью таблиц, но нейросетям незачем ограничивать себя двумя измерениями — поэтому массивы данных выглядят примерно так
В сфере развлечений компьютеры продвинулись не хуже, чем в науке. За счёт машинного обучения им наконец поддались игры, алгоритмы выигрыша для которых придумать ещё сложнее, чем для шахмат. Недавно нейросеть AlphaGo разгромила одного из лучших в мире игроков в го, а программа Libratus победила в профессиональном турнире по покеру. Более того, ИИ уже постепенно пробирается и в кино: например, создатели сериала «Карточный домик» использовали big data при кастинге, чтобы подобрать максимально популярный актёрский состав.
Как и полвека назад, самым перспективным направлением остаётся распознание образов. Рукописный текст или «капча» давно уже не проблема — теперь сети успешно различают людей по фотографиям, учатся определять выражения лиц, сами рисуют котиков и сюрреалистические картины. Сейчас основную практическую пользу из этих развлечений извлекают разработчики беспилотных автомобилей — ведь чтобы оценить ситуацию на дороге, машине нужно очень быстро и точно распознать окружающие предметы. Не отстают и спецслужбы с маркетологами: по обычной записи видеонаблюдения нейронная сеть давно уже может отыскать человека в соцсетях. Поэтому особо недоверчивые заводят себе специальные камуфляжные очки, которые могут обмануть программу.

«Ты всего лишь машина. Только имитация жизни. Разве робот сочинит симфонию? Разве робот превратит кусок холста в шедевр искусства?» («Я, робот»)
Наконец, начинает сбываться и предсказание Розенблатта о самокопирующихся роботах: недавно нейросеть DeepCoder обучили программированию. На самом деле программа пока что просто заимствует куски чужого кода, да и писать умеет только самые примитивные функции. Но разве не с простейшей формулы началась история самих сетей?
Игры с ботами
Развлекаться с недоученными нейросетями очень весело: они порой выдают такие ошибки, что в страшном сне не приснится. А если ИИ начинает учиться, появляется азарт: «Неужто сумеет?» Поэтому сейчас набирают популярность интернет-игры с нейросетями.
Одним из первых прославился интернет-джинн Акинатор, который за несколько наводящих вопросов угадывал любого персонажа. Строго говоря, это не совсем нейросеть, а несложный алгоритм, но со временем он становился всё догадливее. Джинн пополнял базу данных за счёт самих пользователей — и в результате его обучили даже интернет-мемам.
Другое развлечение с «угадайкой» предлагает ИИ от Google: нужно накалякать за двадцать секунд рисунок к заданному слову, а нейросеть потом пробует угадать, что это было. Программа очень смешно промахивается, но порой для верного ответа хватает всего пары линий — а ведь именно так узнаём объекты и мы сами.
Ну и, конечно, в интернете не обойтись без котиков. Программисты взяли вполне серьёзную нейросеть, которая умеет строить проекты фасадов или угадывать цвет на чёрно-белых фотографиях, и обучили её на кошках — чтобы она пыталась превратить любой контур в полноценную кошачью фотографию. Поскольку проделать это ИИ старается даже с квадратом, результат порой достоин пера Лавкрафта!
При таком обилии удивительных новостей может показаться, что искусственный интеллект вот-вот осознает себя и сумеет решить любую задачу. На самом деле не так всё радужно — или, если встать на сторону человечества, не так мрачно. Несмотря на успехи нейросетей, у них накопилось столько проблем, что впереди нас вполне может ждать очередная «зима».
Главная слабость нейросетей в том, что каждая из них заточена под определённую задачу. Если натренировать сеть на фотографиях с котиками, а потом предложить ей задачку «отличи небо от земли», программа не справится, будь в ней хоть миллиард нейронов. Чтобы появились по-настоящему «умные» компьютеры, надо придумать новый алгоритм, объединяющий уже не нейроны, а целые сети, каждая из которых занимается конкретной задачей. Но даже тогда до человеческого мозга компьютерам будет далеко.
Сейчас самой крупной сетью располагает компания Digital Reasoning (хотя новые рекорды появляются чуть ли не каждый месяц) — в их творении 160 миллиардов элементов. Для сравнения: в одном кубическом миллиметре мышиного мозга около миллиарда связей. Причём биологам пока удалось описать от силы участок в пару сотен микрометров, где нашлось около десятка тысяч связей. Что уж говорить о людях!
Один слой умеет узнавать людей, другой — столы, третий — ножи…
Такими 3D-моделями модно иллюстрировать новости о нейросетях, но это всего лишь крошечный участок мышиного мозга
Кроме того, исследователи советуют осторожнее относиться к громким заявлениям Google и IBM. Никаких принципиальных прорывов в «когнитивных вычислениях» с 1980-х годов не произошло: компьютеры всё так же механически обсчитывают входящие данные и выдают результат. Нейросеть способна найти закономерность, которую не заметит человек, — но эта закономерность может оказаться случайной. Машина может подсчитать, сколько раз в твиттере упоминается «Оскар», — но не сможет определить, радуются пользователи результатам или ехидничают над выбором киноакадемии.
Теоретики искусственного интеллекта настаивают, что одну из главных проблем — понимание человеческого языка — невозможно решить простым перебором ключевых слов. А именно такой подход до сих пор используют даже самые продвинутые нейросети.
Сказки про Скайнет

Хотя нам самим сложно удержаться от иронии на тему бунта роботов, серьёзных учёных не стоит даже и спрашивать о сценариях из «Матрицы» или «Терминатора»: это всё равно что поинтересоваться у астронома, видел ли он НЛО. Исследователь искусственного интеллекта Элиезер Юдковски, известный по роману «Гарри Поттер и методы рационального мышления», написал ряд статей, где объяснил, почему мы так волнуемся из-за восстания машин — и чего стоит опасаться на самом деле.
Прежде всего, «Скайнет» приводят в пример так, словно мы уже пережили эту историю и боимся повторения. А всё потому, что наш мозг не умеет отличать выдумки с киноэкранов от жизненного опыта. На самом-то деле роботы никогда не бунтовали против своей программы, и попаданцы не прилетали из будущего. С чего мы вообще взяли, что это реальный риск?
Бояться надо не врагов, а чересчур усердных друзей. У любой нейросети есть мотивация: если ИИ должен гнуть скрепки, то, чем больше он их сделает, тем больше получит «награды». Если дать хорошо оптимизированному ИИ слишком много ресурсов, он не задумываясь переплавит на скрепки всё окрестное железо, потом людей, Землю и всю Вселенную. Звучит безумно — но только на человеческий вкус! Так что главная задача будущих создателей ИИ — написать такой жёсткий этический кодекс, чтобы даже существо с безграничным воображением не смогло найти в нём «дырок».
* * *
Итак, до настоящего искусственного интеллекта пока ещё далеко. С одной стороны над этой проблемой по-прежнему бьются нейробиологи, которые ещё до конца не понимают, как же устроено наше сознание. С другой наступают программисты, которые попросту берут задачу штурмом, бросая на обучение нейросетей всё новые и новые вычислительные ресурсы. Но мы уже живём в прекрасную эпоху, когда машины берут на себя всё больше рутинных задач и умнеют на глазах. А заодно служат людям отличным примером, потому что всегда учатся на своих ошибках.
Сделай сам

Нейронную сеть можно сделать с помощью спичечных коробков — тогда у вас в арсенале появится фокус, которым можно развлекать гостей на вечеринках. Редакция МирФ уже попробовала — и смиренно признаёт превосходство искусственного интеллекта. Давайте научим неразумную материю играть в игру «11 палочек». Правила просты: на столе лежит 11 спичек, и в каждый ход можно взять либо одну, либо две. Побеждает тот, кто взял последнюю. Как же играть в это против «компьютера»? Очень просто.
- Берём 10 коробков или стаканчиков. На каждом пишем номер от 2 до 11.
- Кладём в каждый коробок два камешка — чёрный и белый. Можно использовать любые предметы — лишь бы они отличались друг от друга. Всё — у нас есть сеть из десяти нейронов!
Теперь начинается игра.
- Нейросеть всегда ходит первой. Для начала посмотрите, сколько осталось спичек, и возьмите коробок с таким номером. На первом ходу это будет коробок №11.
- Возьмите из нужного коробка любой камешек. Можно закрыть глаза или кинуть монетку, главное — действовать наугад.
- Если камень белый — нейросеть решает взять две спички. Если чёрный — одну. Положите камешек рядом с коробком, чтобы не забыть, какой именно «нейрон» принимал решение.
- После этого ходит человек — и так до тех пор, пока спички не закончатся.
Ну а теперь начинается самое интересное: обучение. Если сеть выиграла партию, то её надо наградить: кинуть в те «нейроны», которые участвовали в этой партии, по одному дополнительному камешку того же цвета, который выпал во время игры. Если же сеть проиграла — возьмите последний использованный коробок и выньте оттуда неудачно сыгравший камень. Может оказаться, что коробок уже пустой, — тогда «последним» считается предыдущий походивший нейрон. Во время следующей партии, попав на пустой коробок, нейросеть автоматически сдастся.
Вот и всё! Сыграйте так несколько партий. Сперва вы не заметите ничего подозрительного, но после каждого выигрыша сеть будет делать всё более и более удачные ходы — и где-то через десяток партий вы поймёте, что создали монстра, которого не в силах обыграть.
А можно сыграть в эту игру прямо здесь

08.04.2017
Нейросети — это настолько просто, что их можно строить даже из спичечных коробков. Мы решили наглядно показать, как это работает, и сделали для вас маленькую браузерную игру. Попробуйте обучить собственный ИИ!
www.mirf.ru
Искусственные нейронные сети простыми словами / Habr
Когда, за бутылкой пива, я заводил разговор о нейронных сетях — люди обычно начинали боязливо на меня смотреть, грустнели, иногда у них начинал дёргаться глаз, а в крайних случаях они залезали под стол. Но, на самом деле, эти сети просты и интуитивны. Да-да, именно так! И, позвольте, я вам это докажу!
Допустим, я знаю о девушке две вещи — симпатична она мне или нет, а также, есть ли о чём мне с ней поговорить. Если есть, то будем считать это единицей, если нет, то — нулём. Аналогичный принцип возьмем и для внешности. Вопрос: “В какую девушку я влюблюсь и почему?”
Можно подумать просто и бескомпромиссно: “Если симпатична и есть о чём поговорить, то влюблюсь. Если ни то и ни другое, то — увольте.”
Но что если дама мне симпатична, но с ней не о чем разговаривать? Или наоборот?
Понятно, что для каждого из нас что-то одно будет важнее. Точнее, у каждого параметра есть его уровень важности, или вернее сказать — вес. Если помножить параметр на его вес, то получится соответственно “влияние внешности” и “влияние болтливости разговора”.
И вот теперь я с чистой совестью могу ответить на свой вопрос:
“Если влияние харизмы и влияние болтливости в сумме больше значения “влюбчивость” то влюблюсь…”
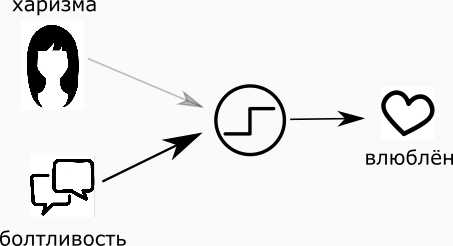
То есть, если я поставлю большой вес “болтологичности” дамы и маленький вес внешности, то в спорной ситуации я влюблюсь в особу, с которой приятно поболтать. И наоборот.
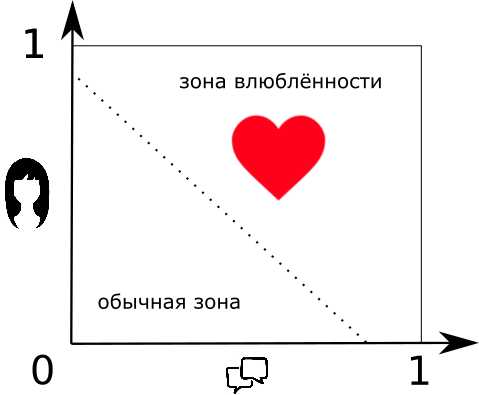
Собственно, это правило и есть нейрон.
Искусственный нейрон — это такая функция, которая преобразует несколько входных фактов в один выходной. Настройкой весов этих фактов, а также порога возбуждения — мы настраиваем адекватность нейрона. В принципе, для многих наука жизни заканчивается на этом уровне, но ведь эта история не про нас, верно?
Сделаем ещё несколько выводов:
- Если оба веса будут малыми, то мне будет сложно влюбиться в кого бы-то ни было.
- Если же оба веса будут чересчур большими, то я влюблюсь хоть в столб.
- Заставить меня влюбиться в столб можно также, понизив порог влюбчивости, но прошу — не делайте со мной этого! Лучше давайте пока забудем про него, ок?
Кстати о пороге
Смешно, но параметр “влюбчивости” называется “порогом возбуждения”. Но, дабы эта статья не получила рейтинг “18+”, давайте договоримся говорить просто “порог”, ок?
Нейронная сеть
Не бывает однозначно симпатичных и однозначно общительных дам. Да и влюблённость влюблённости рознь, кто бы что ни говорил. Потому давайте вместо брутальных и бескомпромиссных “0” и “1”, будем использовать проценты. Тогда можно сказать — “я сильно влюблён (80%), или “эта дама не особо разговорчива (20%)”.
Наш примитивный “нейрон-максималист” из первой части уже нам не подходит. Ему на смену приходит “нейрон-мудрец”, результатом работы которого будет число от 0 до 1, в зависимости от входных данных.
“Нейрон-мудрец” может нам сказать: “эта дама достаточно красива, но я не знаю о чём с ней говорить, поэтому я не очень-то ей и восхищён”
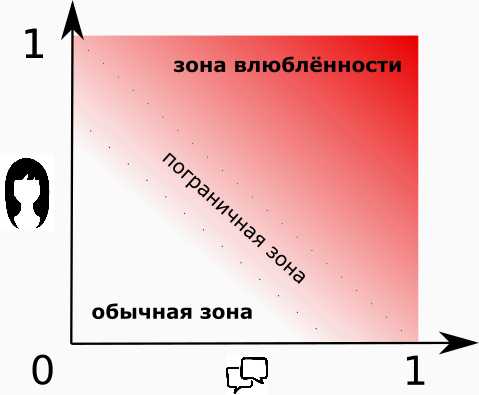
Немного терминологии
К слову говоря, входные факты нейрона называются синапсами, а выходное суждение — аксоном. Связи с положительным весом называются возбуждающими, а с отрицательным — тормозящими. Если же вес равен нулю, то считается, что связи нет (мёртвая связь).
Поехали дальше. Сделаем по этим двум фактам другую оценку: насколько хорошо с такой девушкой работать (сотрудничать)? Будем действовать абсолютно аналогичным образом — добавим мудрый нейрон и настроим веса комфортным для нас образом.
Но, судить девушку по двум характеристикам — это очень грубо. Давайте судить её по трём! Добавим ещё один факт – деньги. Который будет варьироваться от нуля (абсолютно бедная) до единицы (дочь Рокфеллера). Посмотрим, как с приходом денег изменятся наши суждения….
Для себя я решил, что, в плане очарования, деньги не очень важны, но шикарный вид всё же может на меня повлиять, потому вес денег я сделаю маленьким, но положительным.
В работе мне абсолютно всё равно, сколько денег у девушки, поэтому вес сделаю равным нулю.
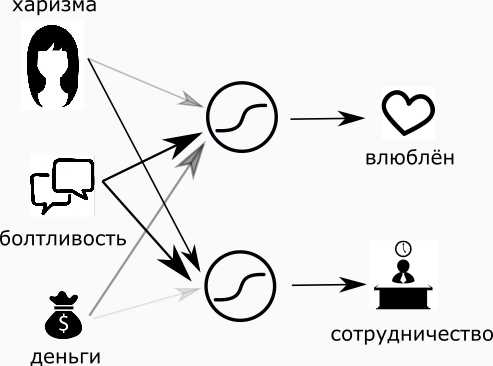
Оценивать девушку только для работы и влюблённости — очень глупо. Давайте добавим, насколько с ней будет приятно путешествовать:
- Харизма в этой задаче нейтральна (нулевой или малый вес).
- Разговорчивость нам поможет (положительный вес).
- Когда в настоящих путешествиях заканчиваются деньги, начинается самый драйв, поэтому вес денег я сделаю слегка отрицательным.
Соединим все эти три схемы в одну и обнаружим, что мы перешли на более глубокий уровень суждений, а именно: от харизмы, денег и разговорчивости — к восхищению, сотрудничеству и комфортности совместного путешествия. И заметьте — это тоже сигналы от нуля до единицы. А значит, теперь я могу добавить финальный “нейрон-максималист”, и пускай он однозначно ответит на вопрос — “жениться или нет”?
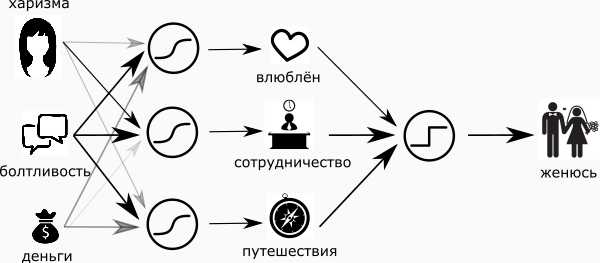
Ладно, конечно же, не всё так просто (в плане женщин). Привнесём немного драматизма и реальности в наш простой и радужный мир. Во-первых, сделаем нейрон «женюсь — не женюсь» — мудрым. Сомнения же присущи всем, так или иначе. И ещё — добавим нейрон «хочу от неё детей» и, чтобы совсем по правде, нейрон “держись от неё подальше».
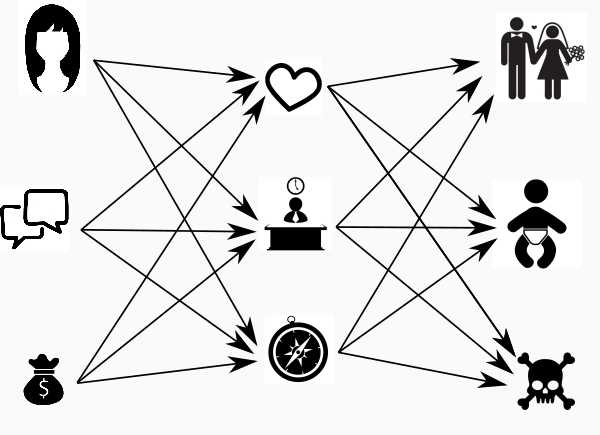
Я ничего не понимаю в женщинах, и поэтому моя примитивная сеть теперь выглядит как картинка в начале статьи.
Входные суждения называются “входной слой”, итоговые — “выходной слой”, а тот, что скрывается посередине, называется «скрытым». Скрытый слой — это мои суждения, полуфабрикаты, мысли, о которых никто не знает. Скрытых слоёв может быть несколько, а может быть и ни одного.
Долой максимализм.
Помните, я говорил об отрицательном влияние денег на моё желание путешествовать с человеком? Так вот — я слукавил. Для путешествий лучше всего подходит персона, у которой денег не мало, и не много. Мне так интереснее и не буду объяснять почему.
Но тут я сталкиваюсь с проблемой:
Если я ставлю вес денег отрицательным, то чем меньше денег — тем лучше для путешествий.
Если положительным, то чем богаче — тем лучше,
Если ноль — тогда деньги “побоку”.
Не получается мне вот так, одним весом, заставить нейрон распознать ситуацию “ни много -ни мало”!
Чтобы это обойти, я сделаю два нейрона — “денег много” и “денег мало”, и подам им на вход денежный поток от нашей дамы.
Теперь у меня есть два суждения: “много” и “мало”. Если оба вывода незначительны, то буквально получится “ни много — ни мало”. То есть, добавим на выход ещё один нейрон, с отрицательными весами:
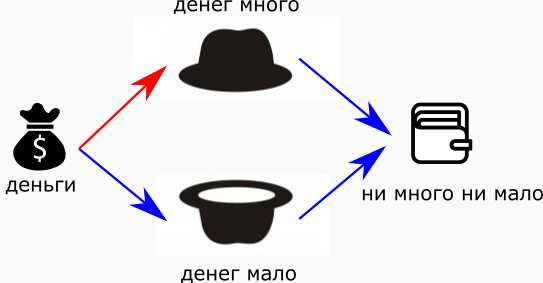
“Нимногонимало”. Красные стрелки — положительные связи, синие — отрицательные
Вообще, это значит, что нейроны подобны элементам конструктора. Подобно тому, как процессор делают из транзисторов, мы можем собрать из нейронов мозг. Например, суждение “Или богата, или умна” можно сделать так:
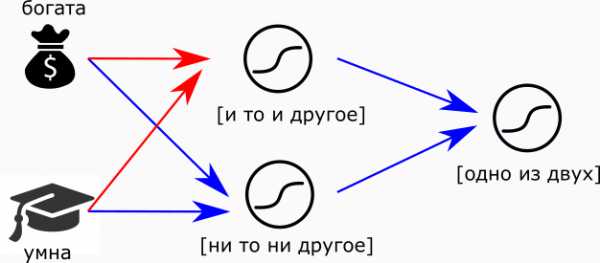
Или-или. Красные стрелки — положительные связи, синие – отрицательные
Или так:
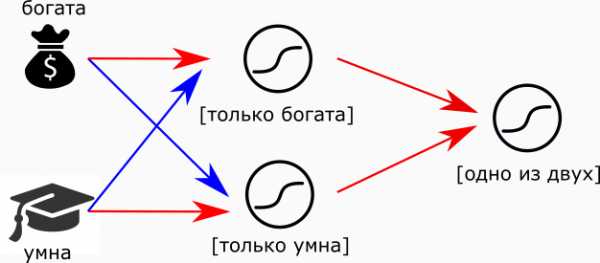
можно заменить “мудрые” нейроны на “максималистов” и тогда получим логический оператор XOR. Главное — не забыть настроить пороги возбуждения.
В отличие от транзисторов и бескомпромиссной логики типичного программиста “если — то”, нейронная сеть умеет принимать взвешенные решения. Их результаты будут плавно меняться, при плавном изменение входных параметров. Вот она мудрость!
Обращу ваше внимание, что добавление слоя из двух нейронов, позволило нейрону “ни много — ни мало” делать более сложное и взвешенное суждение, перейти на новый уровень логики. От “много” или “мало” — к компромиссному решению, к более глубокому, с философской точки зрения, суждению. А что если добавить скрытых слоёв ещё? Мы способны охватить разумом ту простую сеть, но как насчёт сети, у которой есть 7 слоёв? Способны ли мы осознать глубину её суждений? А если в каждом из них, включая входной, около тысячи нейронов? Как вы думаете, на что она способна?
Представьте, что я и дальше усложнял свой пример с женитьбой и влюблённостью, и пришёл к такой сети. Где-то там в ней скрыты все наши девять нейрончиков, и это уже больше похоже на правду. При всём желании, понять все зависимости и глубину суждений такой сети — попросту невозможно. Для меня переход от сети 3х3 к 7х1000 — сравним с осознанием масштабов, если не вселенной, то галактики — относительно моего роста. Попросту говоря, у меня это не получится. Решение такой сети, загоревшийся выход одного из её нейронов — будет необъясним логикой. Это то, что в быту мы можем назвать “интуицией” (по крайней мере – “одно из..”). Непонятное желание системы или её подсказка.
Но, в отличие от нашего синтетического примера 3х3, где каждый нейрон скрытого слоя достаточно чётко формализован, в настоящей сети это не обязательно так. В хорошо настроенной сети, чей размер не избыточен для решения поставленной задачи — каждый нейрон будет детектировать какой-то признак, но это абсолютно не значит, что в нашем языке найдётся слово или предложение, которое сможет его описать. Если проецировать на человека, то это — какая-то его характеристика, которую ты чувствуешь, но словами объяснить не можешь.
Обучение.
Несколькими строчками ранее я обмолвился о хорошо настроенной сети, чем вероятно спровоцировал немой вопрос: “А как мы можем настроить сеть, состоящую из нескольких тысяч нейронов? Сколько “человеколет” и погубленных жизней нужно на это?.. Боюсь предположить ответ на последний вопрос. Куда лучше автоматизировать такой процесс настройки — заставить сеть саму настраивать себя. Такой процесс автоматизации называется обучением. И чтобы дать поверхностное о нём представление, я вернусь к изначальной метафоре об “очень важном вопросе”:
Мы появляемся в этом мире с чистым, невинным мозгом и нейронной сетью, абсолютно не настроенной относительно дам. Её необходимо как-то грамотно настроить, дабы счастье и радость пришли в наш дом. Для этого нам нужен некоторый опыт, и тут есть несколько путей по его добыче:
1) Обучение с учителем (для романтиков). Насмотреться на голливудские мелодрамы и начитаться слезливых романов. Или же насмотреться на своих родителей и/или друзей. После этого, в зависимости от выборки, отправиться проверять полученные знания. После неудачной попытки — повторить всё заново, начиная с романов.
2) Обучение без учителя (для отчаянных экспериментаторов). Попробовать методом “тыка” жениться на десятке-другом женщин. После каждой женитьбы, в недоумение чесать репу. Повторять, пока не поймёшь, что надоело, и ты “уже знаешь, как это бывает”.
3) Обучение без учителя, вариант 2 (путь отчаянных оптимистов). Забить на всё, что-то делать по жизни, и однажды обнаружить себя женатым. После этого, перенастроить свою сеть в соответствие с текущей реальностью, дабы всё устраивало.
Далее, по логике я должен расписать всё это подробно, но без математики это будет слишком философично. Потому считаю, что мне стоит на этом остановиться. Быть может в другой раз?
Всё вышесказанное справедливо для искусственной нейронной сети типа “персептрон”. Остальные сети похожи на нее по основным принципам, но имеют свою нюансы.
Хороших вам весов и отличных обучающих выборок! Ну а если это уже и не нужно, то расскажите об этом кому-нибудь ещё.
ENG version
habr.com
описание простым и понятным языком

Содержание:
В последнее время все чаще и чаще говорят про так званные нейронные сети, дескать вскоре они будут активно применятся и в роботехнике, и в машиностроении, и во многих других сферах человеческой деятельности, ну а алгоритмы поисковых систем, того же Гугла уже потихоньку начинают на них работать. Что же представляют собой эти нейронные сети, как они работают, какое у них применение и чем они могут стать полезными для нас, обо всем этом читайте дальше.
Что такое нейронные сети
Нейронные сети – это одно из направлений научных исследований в области создания искусственного интеллекта (ИИ) в основе которого лежит стремление имитировать нервную систему человека. В том числе ее (нервной системы) способность исправлять ошибки и самообучаться. Все это, хотя и несколько грубо должно позволить смоделировать работу человеческого мозга.
Биологические нейронные сети
Но это определение абзацем выше чисто техническое, если же говорить языком биологии, то нейронная сеть представляет собой нервную систему человека, ту совокупность нейронов в нашем мозге, благодаря которым мы думаем, принимаем те или иные решения, воспринимаем мир вокруг нас.
Биологический нейрон – это специальная клетка, состоящая из ядра, тела и отростков, к тому же имеющая тесную связь с тысячами других нейронов. Через эту связь то и дело передаются электрохимические импульсы, приводящие всю нейронную сеть в состояние возбуждение или наоборот спокойствия. Например, какое-то приятное и одновременно волнующее событие (встреча любимого человека, победа в соревновании и т. д.) породит электрохимический импульс в нейронной сети, которая располагается в нашей голове, что приведет к ее возбуждению. Как следствие, нейронная сеть в нашем мозге свое возбуждение передаст и другим органам нашего тела и приведет к повышенному сердцебиению, более частому морганию глаз и т. д.
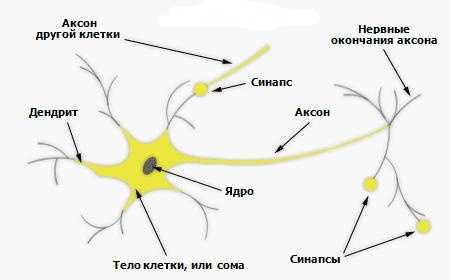
Тут на картинке приведена сильно упрощенная модель биологической нейронной сети мозга. Мы видим, что нейрон состоит из тела клетки и ядра, тело клетки, в свою очередь, имеет множество ответвленных волокон, названых дендритами. Длинные дендриты называются аксонами и имеют протяженность много большую, нежели показано на этом рисунке, посредством аксонов осуществляется связь между нейронами, благодаря ним и работает биологическая нейронная сеть в наших с вами головах.
История нейронных сетей
Какова же история развития нейронных сетей в науке и технике? Она берет свое начало с появлением первых компьютеров или ЭВМ (электронно-вычислительная машина) как их называли в те времена. Так еще в конце 1940-х годов некто Дональд Хебб разработал механизм нейронной сети, чем заложил правила обучения ЭВМ, этих «протокомпьютеров».
Дальнейшая хронология событий была следующей:
- В 1954 году происходит первое практическое использование нейронных сетей в работе ЭВМ.
- В 1958 году Франком Розенблатом разработан алгоритм распознавания образов и математическая аннотация к нему.
- В 1960-х годах интерес к разработке нейронных сетей несколько угас из-за слабых мощностей компьютеров того времени.
- И снова возродился уже в 1980-х годах, именно в этот период появляется система с механизмом обратной связи, разрабатываются алгоритмы самообучения.
- К 2000 году мощности компьютеров выросли настолько, что смогли воплотить самые смелые мечты ученых прошлого. В это время появляются программы распознавания голоса, компьютерного зрения и многое другое.

Искусственные нейронные сети
Под искусственными нейронными сетями принято понимать вычислительные системы, имеющие способности к самообучению, постепенному повышению своей производительности. Основными элементами структуры нейронной сети являются:
- Искусственные нейроны, представляющие собой элементарные, связанные между собой единицы.
- Синапс – это соединение, которые используется для отправки-получения информации между нейронами.
- Сигнал – собственно информация, подлежащая передаче.
Применение нейронных сетей
Область применения искусственных нейронных сетей с каждым годом все более расширяется, на сегодняшний день они используются в таких сферах как:
- Машинное обучение (machine learning), представляющее собой разновидность искусственного интеллекта. В основе его лежит обучение ИИ на примере миллионов однотипных задач. В наше время машинное обучение активно внедряют поисковые системы Гугл, Яндекс, Бинг, Байду. Так на основе миллионов поисковых запросов, которые все мы каждый день вводим в Гугле, их алгоритмы учатся показывать нам наиболее релевантную выдачу, чтобы мы могли найти именно то, что ищем.
- В роботехнике нейронные сети используются в выработке многочисленных алгоритмов для железных «мозгов» роботов.
- Архитекторы компьютерных систем пользуются нейронными сетями для решения проблемы параллельных вычислений.
- С помощью нейронных сетей математики могут разрешать разные сложные математические задачи.
Типы нейронных сетей
В целом для разных задач применяются различные виды и типы нейронных сетей, среди которых можно выделить:
- сверточные нейронные сети,
- реккурентные нейронные сети,
- нейронную сеть Хопфилда.
Далее мы детально остановимся на некоторых из них.
Сверточные нейронные сети
Сверточные сети являются одними из самых популярных типов искусственных нейронных сетей. Так они доказали свою эффективность в распознавании визуальных образов (видео и изображения), рекомендательных системах и обработке языка.
- Сверточные нейронные сети отлично масштабируются и могут использоваться для распознавания образов, какого угодно большого разрешения.
- В этих сетях используются объемные трехмерные нейроны. Внутри одного слоя нейроны связаны лишь небольшим полем, названые рецептивным слоем.
- Нейроны соседних слоев связаны посредством механизма пространственной локализации. Работу множества таких слоев обеспечивают особые нелинейные фильтры, реагирующие на все большее число пикселей.
Рекуррентные нейронные сети
Рекуррентными называют такие нейронные сети, соединения между нейронами которых, образуют ориентировочный цикл. Имеет такие характеристики:
- У каждого соединения есть свой вес, он же приоритет.
- Узлы делятся на два типа, вводные узлы и узлы скрытые.
- Информация в рекуррентной нейронной сети передается не только по прямой, слой за слоем, но и между самими нейронами.
- Важной отличительной особенностью рекуррентной нейронной сети является наличие так званой «области внимания», когда машине можно задать определенные фрагменты данных, требующие усиленной обработки.
Рекуррентные нейронные сети применяются в распознавании и обработке текстовых данных (в частотности на их основе работает Гугл переводчик, алгоритм Яндекс «Палех», голосовой помощник Apple Siri).
Нейронные сети, видео
И в завершение интересное видео о нейронных сетях.
Эта статья доступна на английском языке — Neural Networks.
www.poznavayka.org
Нейронные сети для начинающих. Часть 2 / Habr

Добро пожаловать во вторую часть руководства по нейронным сетям. Сразу хочу принести извинения всем кто ждал вторую часть намного раньше. По определенным причинам мне пришлось отложить ее написание. На самом деле я не ожидал, что у первой статьи будет такой спрос и что так много людей заинтересует данная тема. Взяв во внимание ваши комментарии, я постараюсь предоставить вам как можно больше информации и в то же время сохранить максимально понятный способ ее изложения. В данной статье, я буду рассказывать о способах обучения/тренировки нейросетей (в частности метод обратного распространения) и если вы, по каким-либо причинам, еще не прочитали первую часть, настоятельно рекомендую начать с нее. В процессе написания этой статьи, я хотел также рассказать о других видах нейросетей и методах тренировки, однако, начав писать про них, я понял что это пойдет вразрез с моим методом изложения. Я понимаю, что вам не терпится получить как можно больше информации, однако эти темы очень обширны и требуют детального анализа, а моей основной задачей является не написать очередную статью с поверхностным объяснением, а донести до вас каждый аспект затронутой темы и сделать статью максимально легкой в освоении. Спешу расстроить любителей “покодить”, так как я все еще не буду прибегать к использованию языка программирования и буду объяснять все “на пальцах”. Достаточно вступления, давайте теперь продолжим изучение нейросетей.
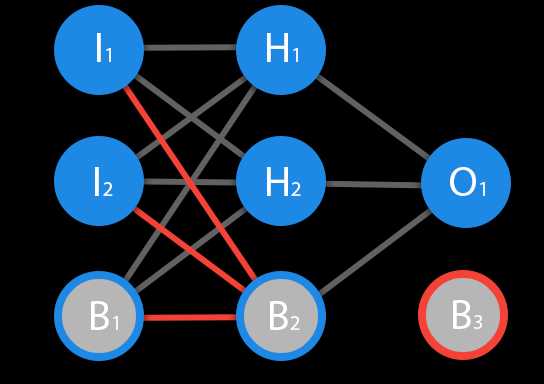
Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь.
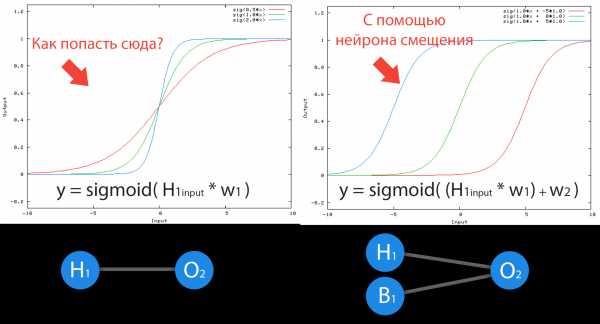
Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу h2, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.
Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес h2, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.
Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.
ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:
input = h2*w1+h3*w2+b3
b3 = bias*w3
Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.
Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:
- Метод обратного распространения (Backpropagation)
- Метод упругого распространения (Resilient propagation или Rprop)
- Генетический Алгоритм (Genetic Algorithm)
Об Rprop и ГА речь пойдет в других статьях, а сейчас мы с вами посмотрим на основу основ — метод обратного распространения, который использует алгоритм градиентного спуска.
Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e).
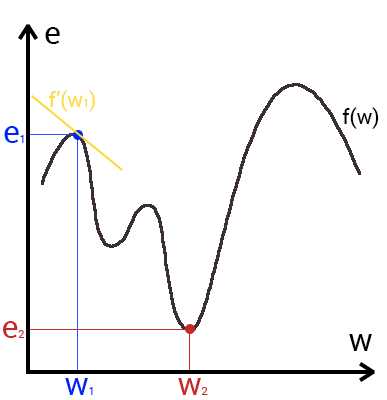
Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.
Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:
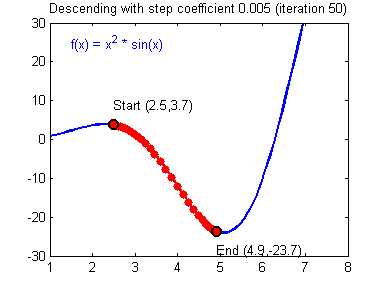
Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:
Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?
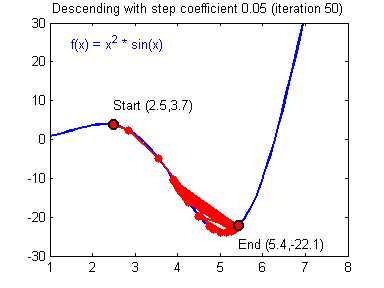
Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже).
Вот мы и дошли до того момента, когда мы можем обсудить, как же все таки сделать так, чтобы ваша НС могла правильно обучаться и давать верные решения. Очень хорошо МОР визуализирован на этой гифке:
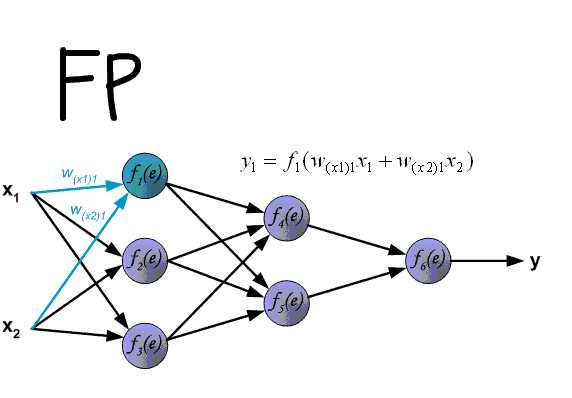
А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).
Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.
Данные задачи из предыдущей статьи
Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.
h2input = 1*0.45+0*-0.12=0.45
h2output = sigmoid(0.45)=0.61
h3input = 1*0.78+0*0.13=0.78
h3output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
O1ideal = 1 (0xor1=1)
Error = ((1-0.33)^2)/1=0.45
Результат — 0.33, ошибка — 45%.
Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение δ (дельта) по формуле 1.
Так как у выходного нейрона нет исходящих синапсов, то мы будем пользоваться первой формулой (δ output), следственно для скрытых нейронов мы уже будем брать вторую формулу (δ hidden). Тут все достаточно просто: считаем разницу между желаемым и полученным результатом и умножаем на производную функции активации от входного значения данного нейрона. Прежде чем приступить к вычислениям я хочу обратить ваше внимание на производную. Во первых как это уже наверное стало понятно, с МОР нужно использовать только те функции активации, которые могут быть дифференцированы. Во вторых чтобы не делать лишних вычислений, формулу производной можно заменить на более дружелюбную и простую формула вида:
Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.РешениеO1output = 0.33
O1ideal = 1
Error = 0.45
δO1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148
На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для h2:Решениеh2output = 0.61
w5 = 1.5
δO1 = 0.148
δh2 = ( (1 — 0.61) * 0.61 ) * ( 1.5 * 0.148 ) = 0.053
Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так:
Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:Решениеh2output = 0.61
δO1 = 0.148
GRADw5 = 0.61 * 0.148 = 0.09
Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом:
Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.
Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, α (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему Δw5.
РешениеE = 0.7Α = 0.3
w5 = 1.5
GRADw5 = 0.09
Δw5(i-1) = 0
Δw5 = 0.7 * 0.09 + 0 * 0.3 = 0.063
w5 = w5 + Δw5 = 1.563
Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для h3.Решениеh3output = 0.69
w6 = -2.3
δO1 = 0.148
E = 0.7
Α = 0.3
Δw6(i-1) = 0
δh3 = ( (1 — 0.69) * 0.69 ) * ( -2.3 * 0.148 ) = -0.07
GRADw6 = 0.69 * 0.148 = 0.1
Δw6 = 0.7 * 0.1 + 0 * 0.3 = 0.07
w6 = w6 + Δw6 = -2.2
И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.Решениеw1 = 0.45, Δw1(i-1) = 0
w2 = 0.78, Δw2(i-1) = 0
w3 = -0.12, Δw3(i-1) = 0
w4 = 0.13, Δw4(i-1) = 0
δh2 = 0.053
δh3 = -0.07
E = 0.7
Α = 0.3
GRADw1 = 1 * 0.053 = 0.053
GRADw2 = 1 * -0.07 = -0.07
GRADw3 = 0 * 0.053 = 0
GRADw4 = 0 * -0.07 = 0
Δw1 = 0.7 * 0.053 + 0 * 0.3 = 0.04
Δw2 = 0.7 * -0.07 + 0 * 0.3 = -0.05
Δw3 = 0.7 * 0 + 0 * 0.3 = 0
Δw4 = 0.7 * 0 + 0 * 0.3 = 0
w1 = w1 + Δw1 = 0.5
w2 = w2 + Δw2 = 0.73
w3 = w3 + Δw3 = -0.12
w4 = w4 + Δw4 = 0.13
Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.РешениеI1 = 1
I2 = 0
w1 = 0.5
w2 = 0.73
w3 = -0.12
w4 = 0.13
w5 = 1.563
w6 = -2.2
h2input = 1 * 0.5 + 0 * -0.12 = 0.5
h2output = sigmoid(0.5) = 0.62
h3input = 1 * 0.73 + 0 * 0.124 = 0.73
h3output = sigmoid(0.73) = 0.675
O1input = 0.62* 1.563 + 0.675 * -2.2 = -0.51
O1output = sigmoid(-0.51) = 0.37
O1ideal = 1 (0xor1=1)
Error = ((1-0.37)^2)/1=0.39
Результат — 0.37, ошибка — 39%.
Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала.
Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).
Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.
Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.
Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.
Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.
Вкратце о каждом методе:
Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел Δw, сразу обнови соответствующий вес.
Пакетный метод же работает по другому. Мы суммируем Δw всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.
Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму Δw всех весов в той или иной группе.
Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:
- Момент и скорость обучения
- Количество скрытых слоев
- Количество нейронов в каждом слое
- Наличие или отсутствие нейронов смещения
В других типах НС присутствуют дополнительные гиперпараметры, но о них мы говорить не будем. Подбор верных гиперпараметров очень важен и будет напрямую влиять на сходимость вашей НС. Понять стоит ли использовать нейроны смещения или нет достаточно просто. Количество скрытых слоев и нейронов в них можно вычислить перебором основываясь на одном простом правиле — чем больше нейронов, тем точнее результат и тем экспоненциально больше время, которое вы потратите на ее обучение. Однако стоит помнить, что не стоит делать НС с 1000 нейронов для решения простых задач. А вот с выбором момента и скорости обучения все чуточку сложнее. Эти гиперпараметры будут варьироваться, в зависимости от поставленной задачи и архитектуры НС. Например, для решения XOR скорость обучения может быть в пределах 0.3 — 0.7, но в НС которая анализирует и предсказывает цену акций, скорость обучения выше 0.00001 приводит к плохой сходимости НС. Не стоит сейчас заострять свое внимание на гиперпараметрах и пытаться досконально понять, как же их выбирать. Это придет с опытом, а пока что советую просто экспериментировать и искать примеры решения той или иной задачи в сети.

Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС.
Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом.
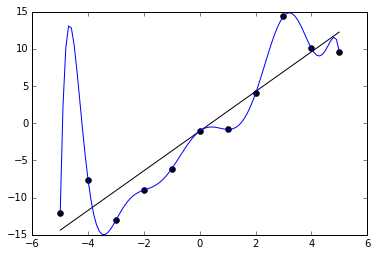
Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться.
Надеюсь эта статья смогла прояснить ключевые моменты такого нелегко предмета, как Нейронные сети. Однако я считаю, что сколько бы ты статей не прочел, без практики такую сложную тему освоить невозможно. Поэтому, если вы только в начале пути и хотите изучить эту перспективную и развивающуюся отрасль, то советую начать практиковаться с написания своей НС, а уже после прибегать к помощи различных фреймворков и библиотек. Также, если вам интересен мой метод изложения информации и вы хотите, чтобы я написал статьи на другие темы связанные с Машинным обучением, то проголосуйте в опросе ниже за ту тему которую вам интересна. До встречи в будущих статьях 🙂
habr.com
Нейросети для начинающих – нейронная сеть для чайников
Искусственная нейронная сеть — совокупность нейронов, взаимодействующих друг с другом. Они способны принимать, обрабатывать и создавать данные. Это настолько же сложно представить, как и работу человеческого мозга. Нейронная сеть в нашем мозгу работает для того, чтобы вы сейчас могли это прочитать: наши нейроны распознают буквы и складывают их в слова.
Искусственная нейронная сеть — это подобие мозга. Изначально она программировалась с целью упростить некоторые сложные вычислительные процессы. Сегодня у нейросетей намного больше возможностей. Часть из них находится у вас в смартфоне. Ещё часть уже записала себе в базу, что вы открыли эту статью. Как всё это происходит и для чего, читайте далее.
С чего всё началось
Людям очень хотелось понять, откуда у человека разум и как работает мозг. В середине прошлого века канадский нейропсихолог Дональд Хебб это понял. Хебб изучил взаимодействие нейронов друг с другом, исследовал, по какому принципу они объединяются в группы (по-научному — ансамбли) и предложил первый в науке алгоритм обучения нейронных сетей.
Спустя несколько лет группа американских учёных смоделировала искусственную нейросеть, которая могла отличать фигуры квадратов от остальных фигур.
Как же работает нейросеть?
Исследователи выяснили, нейронная сеть — это совокупность слоёв нейронов, каждый из которых отвечает за распознавание конкретного критерия: формы, цвета, размера, текстуры, звука, громкости и т. д. Год от года в результате миллионов экспериментов и тонн вычислений к простейшей сети добавлялись новые и новые слои нейронов. Они работают по очереди. Например, первый определяет, квадрат или не квадрат, второй понимает, квадрат красный или нет, третий вычисляет размер квадрата и так далее. Не квадраты, не красные и неподходящего размера фигуры попадают в новые группы нейронов и исследуются ими.
Какими бывают нейронные сети и что они умеют
Учёные развили нейронные сети так, что те научились различать сложные изображения, видео, тексты и речь. Типов нейронных сетей сегодня очень много. Они классифицируются в зависимости от архитектуры — наборов параметров данных и веса этих параметров, некой приоритетности. Ниже некоторые из них.
Свёрточные нейросети
Нейроны делятся на группы, каждая группа вычисляет заданную ей характеристику. В 1993 году французский учёный Ян Лекун показал миру LeNet 1 — первую свёрточную нейронную сеть, которая быстро и точно могла распознавать цифры, написанные на бумаге от руки. Смотрите сами:

Сегодня свёрточные нейронные сети используются в основном с мультимедиными целями: они работают с графикой, аудио и видео.
Рекуррентные нейросети
Нейроны последовательно запоминают информацию и строят дальнейшие действия на основе этих данных. В 1997 году немецкие учёные модифицировали простейшие рекуррентные сети до сетей с долгой краткосрочной памятью. На их основе затем были разработаны сети с управляемыми рекуррентными нейронами.
Сегодня с помощью таких сетей пишутся и переводятся тексты, программируются боты, которые ведут осмысленные диалоги с человеком, создаются коды страниц и программ.
Использование такого рода нейросетей — это возможность анализировать и генерировать данные, составлять базы и даже делать прогнозы.
В 2015 году компания SwiftKey выпустила первую в мире клавиатуру, работающую на рекуррентной нейросети с управляемыми нейронами. Тогда система выдавала подсказки в процессе набранного текста на основе последних введённых слов. В прошлом году разработчики обучили нейросеть изучать контекст набираемого текста, и подсказки стали осмысленными и полезными:

Комбинированные нейросети (свёрточные + рекуррентные)
Такие нейронные сети способны понимать, что находится на изображении, и описывать это. И наоборот: рисовать изображения по описанию. Ярчайший пример продемонстрировал Кайл Макдональд, взяв нейронную сеть на прогулку по Амстердаму. Сеть мгновенно определяла, что находится перед ней. И практически всегда точно:
Нейросети постоянно самообучаются. Благодаря этому процессу:
1. Skype внедрил возможность синхронного перевода уже для 10 языков. Среди которых, на минуточку, есть русский и японский — одни из самых сложных в мире. Конечно, качество перевода требует серьёзной доработки, но сам факт того, что уже сейчас вы можете общаться с коллегами из Японии по-русски и быть уверенными, что вас поймут, вдохновляет.
2. Яндекс на базе нейронных сетей создал два поисковых алгоритма: «Палех» и «Королёв». Первый помогал найти максимально релевантные сайты для низкочастотных запросов. «Палех» изучал заголовки страниц и сопоставлял их смысл со смыслом запросов. На основе «Палеха» появился «Королёв». Этот алгоритм оценивает не только заголовок, но и весь текстовый контент страницы. Поиск становится всё точнее, а владельцы сайтов разумнее начинают подходить к наполнению страниц.
3. Коллеги сеошников из Яндекса создали музыкальную нейросеть: она сочиняет стихи и пишет музыку. Нейрогруппа символично называется Neurona, и у неё уже есть первый альбом:

4. У Google Inbox с помощью нейросетей осуществляется ответ на сообщение. Развитие технологий идет полный ходом, и сегодня сеть уже изучает переписку и генерирует возможные варианты ответа. Можно не тратить время на печать и не бояться забыть какую-нибудь важную договорённость.
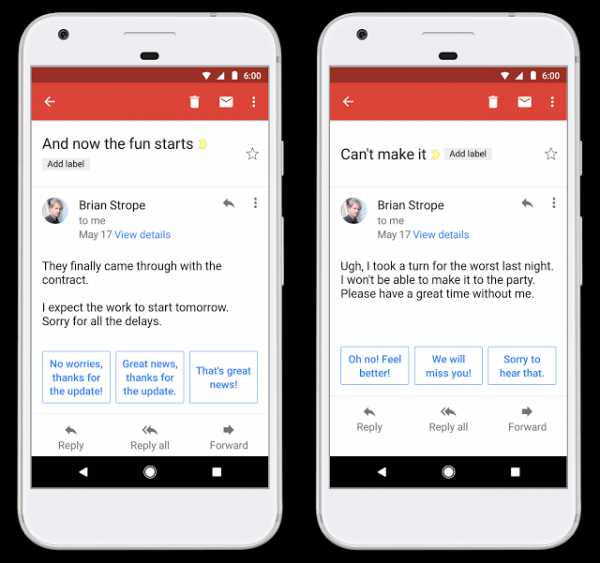
5. YouTube использует нейронные сети для ранжирования роликов, причём сразу по двум принципам: одна нейронная сеть изучает ролики и реакции аудитории на них, другая проводит исследование пользователей и их предпочтений. Именно поэтому рекомендации YouTube всегда в тему.
6. Facebook активно работает над DeepText AI — программой для коммуникаций, которая понимает жаргон и чистит чатики от обсценной лексики.
7. Приложения вроде Prisma и Fabby, созданные на нейросетях, создают изображения и видео:
Colorize восстанавливает цвета на чёрно-белых фото (удивите бабушку!).

MakeUp Plus подбирает для девушек идеальную помаду из реального ассортимента реальных брендов: Bobbi Brown, Clinique, Lancome и YSL уже в деле.

8.
Apple и Microsoft постоянно апгрейдят свои нейронные Siri и Contana.
Искусственная нейронная сеть
Пока они только исполняют наши приказы, но уже в ближайшем будущем начнут проявлять инициативу: давать рекомендации и предугадывать наши желания.
А что ещё нас ждет в будущем?
Самообучающиеся нейросети могут заменить людей: начнут с копирайтеров и корректоров. Уже сейчас роботы создают тексты со смыслом и без ошибок. И делают это значительно быстрее людей. Продолжат с сотрудниками кол-центров, техподдержки, модераторами и администраторами пабликов в соцсетях. Нейронные сети уже умеют учить скрипт и воспроизводить его голосом. А что в других сферах?
Аграрный сектор
Нейросеть внедрят в спецтехнику. Комбайны будут автопилотироваться, сканировать растения и изучать почву, передавая данные нейросети. Она будет решать — полить, удобрить или опрыскать от вредителей. Вместо пары десятков рабочих понадобятся от силы два специалиста: контролирующий и технический.
Медицина
В Microsoft сейчас активно работают над созданием лекарства от рака. Учёные занимаются биопрограммированием — пытаются оцифрить процесс возникновения и развития опухолей. Когда всё получится, программисты смогут найти способ заблокировать такой процесс, по аналогии будет создано лекарство.
Маркетинг
Маркетинг максимально персонализируется. Уже сейчас нейросети за секунды могут определить, какому пользователю, какой контент и по какой цене показать. В дальнейшем участие маркетолога в процессе сведётся к минимуму: нейросети будут предсказывать запросы на основе данных о поведении пользователя, сканировать рынок и выдавать наиболее подходящие предложения к тому моменту, как только человек задумается о покупке.
Ecommerce
Ecommerce будет внедрён повсеместно. Уже не потребуется переходить в интернет-магазин по ссылке: вы сможете купить всё там, где видите, в один клик.
Например, читаете вы эту статью через несколько лет. Очень вам нравится помада на скрине из приложения MakeUp Plus (см. выше). Вы кликаете на неё и попадаете сразу в корзину. Или смотрите видео про последнюю модель Hololens (очки смешанной реальности) и тут же оформляете заказ прямо из YouTube.
Едва ли не в каждой области будут цениться специалисты со знанием или хотя бы пониманием устройства нейросетей, машинного обучения и систем искусственного интеллекта. Мы будем существовать с роботами бок о бок. И чем больше мы о них знаем, тем спокойнее нам будет жить.
P. S.Зинаида Фолс — нейронная сеть Яндекса, пишущая стихи. Оцените произведение, которое машина написала, обучившись на Маяковском (орфография и пунктуация сохранены):
«Это»
это
всего навсего
что-то
в будущем
и мощь
у того человека
есть на свете все или нет
это кровьа вокруг
по рукам
жиреет
слава у
земли
с треском в клюве
Впечатляет, правда?
steptosleep.ru

